How would Alan Turing develop biology?

Alan M. Turing (23 June 1912 – 9 June 1954)
photo taken on March 29th, 1951.

Alan Turing was born 100 years ago, today: June 23rd, 1912. He was a pioneer of computing, cryptography, artificial intelligence, and biology. His most influential work was launching computer science by the definition of computable, introduction of Turing-machine, and solution of the Entscheidungsproblem (Turing, 1936). He served his King and Country in WW2 as the leader of Hut 8 in the Government Code and Cypher School at Bletchley Park. With his genius the British were able to build a semi-automated system for cracking the Enigma machine used for German encryption. After the war he foresaw the connectionist-movement of Cognitive Science by developing his B-type neural network in 1948. He launched the field of artificial intelligence with Computing machinery and intelligence (1950), introducing the still discussed Turing test. In 1952 he published his most cited work: The Chemical Basis of Morphogenesis spurring the development of mathematical biology. Unfortunately, Turing did not leave to see his impact on biology.

In 1952, homosexuality was illegal in the United Kingdom and Turing’s sexual orientation was criminally prosecuted. As an alternative to prison he accepted chemical castration (treatement with female hormones). On June 8th, 1954, just two weeks shy of his 42nd birthday, Alan Turing was found dead in his apartment. He died of cyanide poisoning, and an inquire ruled the death a suicide. A visionary pioneer was taken and we can only wonder: how would Alan Turing develop biology?

In The Chemical Basis of Morphogenesis (1952) Turing asked: how does a spherically symmetric embryo develop into a non-spherically symmetric organism under the action of symmetry-preserving chemical diffusion of morphogens? Morphogens are abstract particles that Turing defined; they can stand in place for any molecules relevant to developmental biology. The key insight that Turing made is that very small stochastic fluctuations in the chemical distribution can be amplified by diffusion to produce stable patterns that break the spherical symmetry. These asymmetric patters are stable and can be time-independent (except a slow increase in intensity), although with three or more morphogens there is also the potential for time-varying patterns.

The beauty of Turing’s work was in its abstraction and simplicity. He modeled the question generally via Chemical diffusion equations and instantiated his model by considering specific arrangements of cells like a discrete cycle, and a continuous ring of tissue. He proved results that were general and qualitative in nature. On more complicated models he also encouraged a numeric quantitative approach to be carried out on the computer he helped develop. It is these rigorous qualitative statements that have become the bread-and-butter of theoretical computer science (TCS).

For me, rigorous qualitative statements (valid for various constants and parameters) instead of quantitative statements based on specific (in some fields: potentially impossible to measure) constant and parameters is one of the two things that sets TCS apart from theoretical physics. The other key feature is that TCS deals with discrete objects of arbitrarily large size, while (classical) physics assumes that the relevant behavior can be approximated by continuous variables. The differential equation approach of physics can provide useful approximations such as replicator dynamics (example applications: perception-deception and cost-of-agency), I think it is fundamentally limited. Differential equations should only be used for intuition in fields like theoretical biology. Although Turing did not get a chance to pursue this avenue, I think that he would have pushed biology into the direction of using more discrete models.

Shnerb et al. (2000) make a good point for the importance of discrete models. The model is of spatial diffusion with two populations: catalyst A that never expires and a population B — agents of which expire at a constant rate and use A to catalyze reproduction. The authors use the standard mean-field diffusion approach to look at the parameter range where the abundance of A is not high enough to counteract the death rate of B agents. The macro-dynamic differential equation approach predicts extinction of the B-population at an exponential rate. However, when the model is simulated at micro-dynamic level with discrete agents, then there is no extinction. Clumps of B agents form and follow individual A agents as they follow Brownian motion through the population. The result is an abundance of life (B agents) at the macro-scale in contrast to the continuous approximation. This is beautifully summarized by Shnerb et al. (2000) in the figure below.

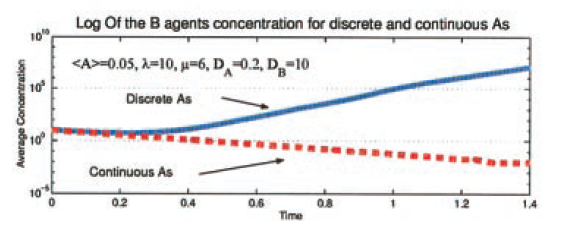
Figure 1 from Shnerb et al. (2000) showing Log of B agent concentration versus time for discrete (solid blue line) and continues (dotted red line) models.

Like Turing’s (1952) approach, the discrete model also shows clumping and symmetry breaking. However, the requirements are not as demanding as what Turing developed. Thus, it is natural to expect that Turing would have found similar models if he continued his work on morphogenesis. This is made more likely by Turing’s exploration of discrete computer models of Artificial Life prior to his death. I think that he would have developed biology by promoting the approach of theoretical computer science: simple abstract models that lead to rigorous qualitative results about discrete structures; Alan Turing would view biology through algorithmic lenses. Since he is no longer with us, I hope that myself and others can carry on his vision.

References

Shnerb NM, Louzoun Y, Bettelheim E, & Solomon S (2000). The importance of being discrete: Life always wins on the surface. Proceedings of the National Academy of Sciences of the United States of America, 97 (19), 10322-4 PMID: 10962027

Turing, A. M. (1936). On Computable Numbers, with an Application to the Entscheidungsproblem. Proceedings of the London Mathematical Society 2(42): 230–65.

Turing, A. M. (1950) Computing Machinery and Intelligence. Mind.

Turing, A. M. (1952). The Chemical Basis of Morphogenesis. Philosophical Transactions of the Royal Society of London 237 (641): 37–72. DOI:10.1098/rstb.1952.0012