Allegory of the replication crisis in algorithmic trading

One of the most interesting ongoing problems in metascience right now is the replication crisis. This a methodological crisis around the difficulty of reproducing or replicating past studies. If we cannot repeat or recreate the results of a previous study then it casts doubt on if those ‘results’ were real or just artefacts of flawed methodology, bad statistics, or publication bias. If we view science as a collection of facts or empirical truths than this can shake the foundations of science.

The replication crisis is most often associated with psychology — a field that seems to be having the most active and self-reflective engagement with the replication crisis — but also extends to fields like general medicine (Ioannidis, 2005a,b; 2016), oncology (Begley & Ellis, 2012), marketing (Hunter, 2001), economics (Camerer et al., 2016), and even hydrology (Stagge et al., 2019).

When I last wrote about the replication crisis back in 2013, I asked what science can learn from the humanities: specifically, what we can learn from memorable characters and fanfiction. From this perspective, a lack of replication was not the disease but the symptom of the deeper malady of poor theoretical foundations. When theories, models, and experiments are individual isolated silos, there is no inherent drive to replicate because the knowledge is not directly cumulative. Instead of forcing replication, we should aim to unify theories, make them more precise and cumulative and thus create a setting where there is an inherent drive to replicate.

More importantly, in a field with well-developed theory and large deductive components, a study can advance the field even if its observed outcome turns out to be incorrect. With a cumulative theory, it is more likely that we will develop new techniques or motivate new challenges or extensions to theory independent of the details of the empirical results. In a field where theory and experiment go hand-in-hand, a single paper can advance both our empirical grounding and our theoretical techniques.

I am certainly not the only one to suggest that a lack of unifying, common, and cumulative theory as the cause for the replication crisis. But how do we act on this?

Can we just start mathematical modelling? In the case of the replicator crisis in cancer research, will mathematical oncology help?

Not necessarily. But I’ll come back to this at the end. First, a story.

Let us look at a case study: algorithmic trading in quantitative finance. This is a field that is heavy in math and light on controlled experiments. In some ways, its methodology is the opposite of the dominant methodology of psychology or cancer research. It is all about doing math and writing code to predict the markets.

Yesterday on /r/algotrading, /u/chiefkul reported on his effort to reproduce 130+ papers about “predicting the stock market”. He coded them from scratch and found that “every single paper was either p-hacked, overfit [or] subsample[d] …OR… had a smidge of Alpha [that disappears with transaction costs]”.

There’s a replication crisis for you. Even the most pessimistic readings of the literature in psychology or medicine produce significantly higher levels of successful replication. So let’s dig in a bit.

Double-entry bookkeeping and Galileo: abstraction vs idealization

Two weeks ago, I wrote a post on how abstract is not the opposite of empirical. In that post, I distinguished between the colloquial meaning of abstract and the ‘true’ meaning used by computer scientists. For me, abstraction is defined by multiple realizability. An abstract object can have many implementations. The concrete objects that implement an abstraction might differ from each other in various — potentially drastic — ways but if the implementations are ‘correct’ then the ways in which they differ are irrelevant to the conclusions drawn from the abstraction.

I contrasted this comp sci view with a colloquial sense that I attributed to David Basanta. I said this colloquial sense was just that an abstract model is ‘less detailed’.

In hindsight, I think this colloquial sense was a straw-man and doesn’t do justice to David’s view. It isn’t ignoring any detail that makes something colloquially abstract. Rather, it is ignoring ‘the right sort of’ detail in the ‘right sort of way’. It is about making an idealization meant to arrive at some essence of a (class of) object(s) or a process. And this idealization view of abstraction has a long pedigree.

In this post, I want to provide a semi-historical discussion of the the difference between (comp sci) abstraction vs idealization. I will focus on double-entry bookkeeping as a motivation. Now, this might not seem relevant to science, but for Galileo it was relevant. He expressed his views on (proto-)scientific abstraction by analogy to bookkeeping. And in expressing his view, he covered both abstraction and idealization. In the process, he introduced both good ideas and bad ones. They remain with us today.

Cross-validation in finance, psychology, and political science

A large chunk of machine learning (although not all of it) is concerned with predictive modeling, usually in the form of designing an algorithm that takes in some data set and returns an algorithm (or sometimes, a description of an algorithm) for making predictions based on future data. In terminology more friendly to the philosophy of science, we may say that we are defining a rule of induction that will tell us how to turn past observations into a hypothesis for making future predictions. Of course, Hume tells us that if we are completely skeptical then there is no justification for induction — in machine learning we usually know this as a no-free lunch theorem. However, we still use induction all the time, usually with some confidence because we assume that the world has regularities that we can extract. Unfortunately, this just shifts the problem since there are countless possible regularities and we have to identify ‘the right one’.

Thankfully, this restatement of the problem is more approachable if we assume that our data set did not conspire against us. That being said, every data-set, no matter how ‘typical’ has some idiosyncrasies, and if we tune in to these instead of ‘true’ regularity then we say we are over-fitting. Being aware of and circumventing over-fitting is usually one of the first lessons of an introductory machine learning course. The general technique we learn is cross-validation or out-of-sample validation. One round of cross-validation consists of randomly partitioning your data into a training and validating set then running our induction algorithm on the training data set to generate a hypothesis algorithm which we test on the validating set. A ‘good’ machine learning algorithm (or rule for induction) is one where the performance in-sample (on the training set) is about the same as out-of-sample (on the validating set), and both performances are better than chance. The technique is so foundational that the only reliable way to earn zero on a machine learning assignments is by not doing cross-validation of your predictive models. The technique is so ubiquotes in machine learning and statistics that the StackExchange dedicated to statistics is named CrossValidated. The technique is so…

You get the point.

If you are a regular reader, you can probably induce from past post to guess that my point is not to write an introductory lecture on cross validation. Instead, I wanted to highlight some cases in science and society when cross validation isn’t used, when it needn’t be used, and maybe even when it shouldn’t be used.

Big data, prediction, and scientism in the social sciences

Much of my undergrad was spent studying physics, and although I still think that a physics background is great for a theorists in any field, there are some downsides. For example, I used to make jokes like: “soft isn’t the opposite of hard sciences, easy is.” Thankfully, over the years I have started to slowly grow out of these condescending views. Of course, apart from amusing anecdotes, my past bigotry would be of little importance if it wasn’t shared by a surprising number of grown physicists. For example, Sabine Hossenfelder — an assistant professor of physics in Frankfurt — writes in a recent post:

It isn’t so surprising that social scientists themselves are unhappy because the boat of inadequate skills is sinking in the data sea and physics envy won’t keep it afloat. More interesting than the paddling social scientists is the public opposition to the idea that the behavior of social systems can be modeled, understood, and predicted.

As a blogger I understand that we can sometimes be overly bold and confrontational. As an informal medium, I have no fundamental problem with such strong statements or even straw-men if they are part of a productive discussion or critique. If there is no useful discussion, I would normally just make a small comment or ignore the post completely, but this time I decided to focus on Hossenfelder’s post because it highlights a common symptom of interdisciplinitis: an outsider thinking that they are addressing people’s critique — usually by restating an obvious and irrelevant argument — while completely missing the point. Also, her comments serve as a nice bow to tie together some thoughts that I’ve been wanting to write about recently.

Liquidity hoarding and systemic failure in the ecology of banks

As you might have guessed from my recent posts, I am cautious in trying to use mathematics to build insilications for predicting, profiting from, or controlling financial markets. However, I realize the wealth of data available on financial networks and interactions (compared to similar resources in ecology, for example) and the myriad of interesting questions about both economics and humans (and their institutions) more generally that understanding finance can answer. As such, I am more than happy to look at heuristics and other toy models in order to learn about financial systems. I am particularly interested in understanding the interplay between individual versus systemic risk because of analogies to social dilemmas in evolutionary game theory (and the related discussions of individual vs. inclusive vs. group fitness) and recently developed connections with modeling in ecology.

Three-month Libor-overnight Interest Swap based on data from Bloomberg and figure 1 of Domanski & Turner (2011). The vertical line marks 15 September 2008 — the day Lehman Brothers filed for bankruptcy.

A particular interesting phenomenon to understand is the sudden liquidity freeze during the recent financial crisis — interbank lending beyond very short maturities virtually disappeared, three-month Libor (a key benchmarks for interest rates on interbank loans) skyrocketed, and the world banking system ground to a halt. The proximate cause for this phase transition was the bankruptcy of Lehman Brothers — the fourth largest investment bank in the US — at 1:45 am on 15 September 2008, but the real culprit lay in build up of unchecked systemic risk (Ivashina & Scharfstein, 2010; Domanski & Turner, 2011; Gorton & Metrick, 2012). Since I am no economist, banker, or trader, the connections and simple mathematical models that Robert May has been advocating (e.g. May, Levin, & Sugihara (2008)) serve as my window into this foreign land. The idea of a good heuristic model is to cut away all non-essential features and try to capture the essence of the complicated phenomena needed for our insight. In this case, we need to keep around an idealized version of banks, their loan network, some external assets with which to trigger an initial failure, and a way to represent confidence. The question then becomes: under what conditions is the initial failure contained to one or a few banks, and when does it paralyze or — without intervention — destroy the whole financial system?

Mathematics in finance and hiding lies in complexity

Sir Andrew Wiles

Mathematics has a deep and rich history, extending well beyond the 16th century start of the scientific revolution. Much like literature, mathematics has a timeless quality; although its trends wax and wane, no part of it becomes out-dated or wrong. What Diophantus of Alexandria wrote on solving algebraic equations in the 3rd century was still as true in the 16th, 17th, or today. In fact, it was in 1637 in the margins of Diophantus’ Arithmetica that Pierre de Fermat scribbled the statement of his Last Theorem. that the margin was too narrow to contain^[1]. In modern notation it is probably one of the most famous Diophantine equations with the assertion that it has no solutions for and as positive integers. A statement that almost anybody can understand, but one that is far from easy to prove or even approach^[2].

Randomness, necessity, and non-determinism

If we want to talk philosophy then it is necessary to mention Aristotle. Or is it just a likely beginning? For Aristotle, there were three types of events: certain, probable, and unknowable. Unfortunately for science, Aristotle considered the results of games of chance to be unknowable, and probability theory started — 18 centuries later — with the analysis of games of chance. This doomed much of science to an awkward fetishisation of probability, an undue love of certainty, and unreasonable quantification of the unknowable. A state of affairs that stems from our fear of admitting when we are ignorant, a strange condition given that many scientists would agree with Feynman’s assessment that one of the main features of science is acknowledging our ignorance:

Unfortunately, we throw away our ability to admit ignorance when we assign probabilities to everything. Especially in settings where there is no reason to postulate an underlying stochastic generating process, or a way to do reliable repeated measurements. “Foul!” you cry, “Bayesians talk about beliefs, and we can hold beliefs about single events. You are just taking the dated frequentist stance.” Well, to avoid the nonsense of the frequentist vs. Bayesian debate, let me take literately the old adage “put your money where you mouth is” and use the fundamental theorem of asset pricing to define probability. I’ll show an example of a market we can’t price, and ask how theoretical computer science can resolve our problem with non-determinism.

Black swans and Orr-Gillespie theory of evolutionary adaptation

The internet loves fat tails, it is why awesome things like wikipedia, reddit, and countless kinds of StackExchanges exist. Finance — on the other hand — hates fat tails, it is why VaR and financial crises exist. A notable exception is Nassim Taleb who became financially independent by hedging against the 1987 financial crisis, and made a multi-million dollar fortune on the recent crisis; to most he is known for his 2007 best-selling book The Black Swan. Taleb’s success has stemmed from his focus on highly unlikely events, or samples drawn from far on the tail of a distribution. When such rare samples have a large effect then we have a Black Swan event. These are obviously important in finance, but Taleb also stresses its importance to the progress of science, and here I will sketch a connection to the progress of evolution.

Machine learning and prediction without understanding

Big data is the buzzword du jour, permeating from machine learning to hadoop powered distributed computing, from giant scientific projects to individual social science studies, and from careful statistics to the witchcraft of web-analytics. As we are overcome by petabytes of data and as more of it becomes public, it is tempting for a would-be theorist to simply run machine learning and big-data algorithms on these data sets and take the computer’s conclusions as understanding. I think this has the danger of overshadowing more traditional approaches to theory and the feedback between theory and experiment.

Individual versus systemic risk in asset allocation

Proponents of free markets often believe in an “invisible hand” that guides an economic system without external controls like government regulations. Therefore a highly efficient economic equilibrium can be created if all market participants act purely out of self-interest. In the paper titled “Individual versus systemic risk and the Regulator’s Dilemma.”, Beale et al. (2011) applied agent-based simulations to show that a system of financial institutions attempting to minimize their own risk of failure may not minimize the risk of failure of the entire system. In addition, the authors have suggested several ways to limit the financial institutions in order to lower the risk of failure for the financial system. Their suggestion responds directly to the regulatory challenges during the recent financial crisis where failures of some institutions have endangered the financial system and even the global economy.

It’s easy to get tangled up trying to regulate banks.

To illustrate the point of individual optimality versus the system optimality, the paper makes simple assumptions of the financial system and its participants. In a world of 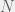independent banks and 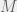assets, each of the 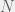banks seeks to invest its resources into these 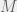assets from time 0 to time 1. The 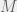returns on assets are assumed to be independently and identically distributed following a student’s t-distribution with a degree of freedom of 1.5. If a bank’s loss exceeds a certain threshold, it fails. Due to this assumption, each bank’s optimal allocation (to minimize it’s chance of failure) is to invest equally in each asset.

However, a regulator is concerned with the failure of the financial system instead of the failure of any individual bank. To incorporate this idea, the paper suggests a cost function for the regulator: where 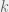is the number of failed banks. This cost function is the only coupling between banks in the model. If , this cost function implies each additional bank failure “costs” the system more (one can tell by taking the derivative 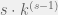, which is an increasing function in 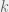if ). As increases from 1, the systematic optimal allocation of all the banks starts to deviate further away from the individual optimal allocation of the banks. When is 2, the systematic optimal allocation for each bank is to invest entirely in one asset, a drastic contrast to the individual optimal allocation (investing equally in each asset). In this situation, the safest investment allocation for the system leads to the riskiest investment allocation for the individual bank.

While the idea demonstrated above is interesting, the procedure is unnecessarily complex. The assumption of student t distribution with degree of freedom of 1.5 is far too broad of an assumption for the distribution of financial assets. However, the distribution does not have the simplicity of Bernoulli or Gaussian distributions to arrive at analytical solutions (See Artem’s question on toy models of asset returns for more discussion). One simple example would be bonds whose principal and coupon payments of the bond are either paid to the bondholder in full or partially paid in the event of a default. Therefore bond is not close to a t-distribution. Other common assets such as mortgages and consumer loans are not t-distribution either. Therefore the assumption of t-distribution does not come close to capturing the probabilistic nature of many major financial assets. The assumption of t-distribution does not provide any additional accuracy to simpler assumptions of Gaussian or Bernoulli distributions. Assumption of Gaussian distribution or Bernoulli distributions, on the other hand, is at least capable of providing analytical solutions without the tedious simulations.

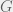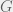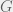The authors define two parameters and in an attempt to constrain the banks to have systematically optimal allocations. denotes the average distance of asset allocations between each pair of banks. denotes the distance between the average allocations across banks and the individual optimal allocation. When is increasing from 1, it was found that bank allocations with a higher and a near-zero are best for the system. To show the robustness of these two parameters, the authors varied other parameters such as number of assets, number of banks, the distributions of the assets, correlation between the assets, and the form of the regulator’s cost function. They found lower systematic risk for the banking system by enforcing a near zero 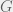and higher . This result implies that the banks should concentrate in their own niche of financial assets, but the aggregate system should still have optimal asset allocations.

Based on the paper, it may appear that the systematic risk of failure can be reduced in the financial system by controlling for parameters and 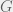(though without analytical solutions). Such controls have to be enforced by an omnipotent “regulator” with perfect information on the exact probabilistic nature of the financial products and the individual optimal allocations. Moreover, this “regulator” must also have unlimited political power to enforce its envisioned allocations. This is far from reality. Financial products are different in size and riskiness, and there is continuous creation of new financial products. Regulators such as the Department of Treasury, SEC, and Federal Reserve also have very limited political power. For example, these regulators were not legally allowed to rescue Lehman Brothers whose failure led to the subsequent global credit and economic crisis. The entire paper can be boiled down to one simple idea: optimal actions for the individuals might not be optimal for the system, but if there is an all-powerful regulator who forces the individuals to act optimally for the system, the system will be more stable. This should come as no surprise to regular readers of this blog, since evolutionary game theory deals with this exact dilemma when looking for cooperation. This main result is rather trivial, but opens ideas for more realistic simulations. One idea would be to remove or weaken the element of “regulator” and add incentives for banks to act more systematically optimal. It would be interesting to look at how banks can act under these circumstances and whether or not their actions can lead to a systematically optimal equilibrium.

One key aspect of a systematic failure is not the simultaneous failure of many assets. There are two important aspects of bank operations. Banks operate by taking funding from clients to invest in riskier assets. This operation requires strong confidence in the bank’s strength to avoid unexpected withdrawals or the ability to sell these assets to pay back the clients. Secondly banks obtain short-term loans from each other by putting up assets as collateral. This connects the banks more strongly than a simple regulator cost function, creating a banking ecosystem.

The strength of the inter-bank connections depends on value of the collateral. In the event of catastrophic losses of subprime loans by some banks, confidence in these banks are shaken and the value of assets start to come down. A bank’s clients may start to withdraw their money and the bank sells its assets to meet its clients’ demands, further depressing the prices of the assets sometimes leading to a fire sale. Other banks would start asking for more and higher quality collateral due to the depressed prices from the sell-off. The bank’s high-quality assets and cash may subsequently become strained leading to further worry about the bank’s health and more client withdrawals and collateral demands. Lack of confidence in one bank’s survival leads to worries about the other banks that have lent to that bank triggering a fresh wave of withdrawals and collateral demands. Even healthy banks can be ruined in a matter of days by a widespread panic.

As a result, the inter-bank dealings are instrumental in the event of systematic failure. Beale et al. (2011) intentionally sidestepped this inter-bank link to arrive at their result purely from a perspective of asset failure. But, the inter-bank link was the most important factor in creating mass failure of the financial system. It is because of this link that failure of one asset (subprime mortgages) managed to nearly bring down the financial systems in the entire developed world. Not addressing the inter-bank link is simply not addressing the financial crisis at all.

Beale N., Rand D.G., Battey H., Croxson K., May R.M. & Nowak M.A. (2011). Individual versus systemic risk and the Regulator’s Dilemma, Proceedings of the National Academy of Sciences, 108 (31) 12647-12652. DOI: 10.1073/pnas.1105882108