Plato and the working mathematician on Truth and discourse

Plato’s writing and philosophy are widely studied in colleges, and often turned to as founding texts of western philosophy. But if we went out looking for people that embraced the philosophy — if we went out looking for actual Platonist — then I think we would come up empty-handed. Or maybe not?

A tempting counter-example is the mathematician.

It certainly seems that to do mathematics, it helps to imagine the objects that you’re studying as inherently real but in a realm that is separate from your desk, chair and laptop. I am certainly susceptible to this thinking. Some mathematicians might even claim that they are mathematical platonists. But there is sometimes reasons to doubt the seriousness of this claim. As Reuben Hersh wrote in Some Proposals for Reviving the Philosophy of Mathematics:

the typical “working mathematician” is a Platonist on weekdays and a formalist on Sundays. That is, when he is doing mathematics, he is convinced that he is dealing with an objective reality whose properties he is attempting to determine. But then, when challenged to give a philosophical account of this reality, he finds it easiest to pretend that he does not believe in it after all.

What explains this discrepency? Is mathematical platonism — or a general vague idealism about mathematical objects — compatible with the actual philosophy attributed to Plato? This is the jist of a question that Conifold asked on the Philosophy StackExchange almost 4 years ago.

In this post, I want to revisit and share my answer. This well let us contrast mathematical platonism with a standard reading of Plato’s thought. After, I’ll take some helpful lessons from postmodernism and consider an alternative reading of Plato. Hopefully this PoMo Plato can suggest some fun thoughts on the old debate on discovery vs invention in mathematics, and better flesh out my Kantian position on the Church-Turing thesis.

Passive vs. active reading and personalization

As you can probably tell, dear reader, recently I have been spending too much time reading and not enough time writing. The blog has been silent. What better way to break this silence than to write a defense of reading? Well, sort of. It would not be much of an eye-opener for you — nor a challenge for me — to simply argue for reading. Given how you are consuming this content, you probably already think that the written word is a worthwhile medium. Given how I am presenting myself, I probably think the same. But are our actions really an endorsement of reading or just the form of communication we begrudgingly resort to because of a lack of better alternatives?

Ostensibly this post will be a qualified defense against an attack on reading by Roger Schank at Education Outrage. Although it is probably best to read it as just a series of reflections on my own experience.^[1]

I will focus on the medium-independent aspects of learning that I think give weight to Schank’s argument: the distinction between passive and active learning, and the level of personalization. This will be followed next week by a tangent discussion on the importance of emotional aspects of the text, and close with some reflections on the role of literary value, historic context, and fiction in philosophical arguments. This last point is prompted more by my recent readings of Plato than by Schank. In other words, much like last year, I will rely on Socrates to help get me out of a writing slump.

Why academics should blog and an update on readership

It’s that time again, TheEGG has passed a milestone — 150 posts under our belt!– and so I feel obliged to reflect on blogging plus update the curious on the readerships statistics.

About a month ago, Nicholas Kristof bemoaned the lack of public intellectuals in the New York Times. Some people responded with defenses of the ‘busy academic’, and others agreement but with a shift of conversation medium to blogs from the more traditional media Kristof was focused on. As a fellow blogger, I can’t help but support this shift, but I also can’t help but notice the conflation of two very different notions: the public intellectual and the public educator.

Interface theory of perception can overcome the rationality fetish

I might be preaching to the choir, but I think the web is transformative for science. In particular, I think blogging is a great form or pre-pre-publication (and what I use this blog for), and Q&A sites like MathOverflow and the cstheory StackExchange are an awesome alternative architecture for scientific dialogue and knowledge sharing. This is why I am heavily involved with these media, and why a couple of weeks ago, I nominated myself to be a cstheory moderator. Earlier today, the election ended and Lev Reyzin and I were announced as the two new moderators alongside Suresh Venkatasubramanian, who is staying on to for continuity and to teach us the ropes. I am extremely excited to work alongside Suresh and Lev, and to do my part to continue devoloping the great community that we nurtured over the last three and a half years.

However, I do expect to face some challenges. The only critique raised against our outgoing moderators, was that an argumentative attitude that is acceptable for a normal user can be unfitting for a mod. I definitely have an argumentative attitude, and so I will have to be extra careful to be on my best behavior.

Thankfully, being a moderator on cstheory does not change my status elsewhere on the website, so I can continue to be a normal argumentative member of the Cognitive Sciences StackExchange. That site is already home to one of my most heated debates against the rationality fetish. In particular, I was arguing against the statement that “a perfect Bayesian reasoner [is] a fixed point of Darwinian evolution”. This statement can be decomposed into two key assumptions: a (1) perfect Bayesian reasoner makes the most veridical decisions given its knowledge, and (2) veridicity has greater utility for an agent and will be selected for by natural selection. If we accept both premises then a perfect Bayesian reasoner is a fitness-peak. Of course, as we learned before: even if something is a fitness-peak doesn’t mean we can ever find it.

We can also challenge both of the assumptions (Feldman, 2013); the first on philosophical grounds, and the second on scientific. I want to concentrate on debunking the second assumption because it relates closely to our exploration of objective versus subjective rationality. To make the discussion more precise, I’ll approach the question from the point of view of perception — a perspective I discovered thanks to TheEGG blog; in particular, the comments of recent reader Zach M.

What is the algorithmic lens?

If you are a regular reader then you are probably familiar with my constant mention of the algorithmic lens. I insist that we must apply it to everything: biology, cognitive science, ecology, economics, evolution, finance, philosophy, probability, and social science. If you’re still reading this then you have incredible powers to resist clicking links. Also, you are probably mathematically inclined and appreciate the art of good definitions. As such, you must be incredibly irked by my lack of attempt at explicitly defining the algorithmic lens. You are not the only one, dear reader, there have been many times where I have been put on the spot and asked to define this ‘algorithmic lens’. My typical response has been the blank stare; not the “oh my, why don’t you already know this?” stare, but the “oh my, I don’t actually know how to define this” stare. Like the artist, continental philosopher, or literary critic, I know how ‘algorithmic lens’ makes me feel and what it means to me, but I just can’t provide a binding definition. Sometimes I even think it is best left underspecified, but I won’t let that thought stop me from attempting a definition.

Black swans and Orr-Gillespie theory of evolutionary adaptation

The internet loves fat tails, it is why awesome things like wikipedia, reddit, and countless kinds of StackExchanges exist. Finance — on the other hand — hates fat tails, it is why VaR and financial crises exist. A notable exception is Nassim Taleb who became financially independent by hedging against the 1987 financial crisis, and made a multi-million dollar fortune on the recent crisis; to most he is known for his 2007 best-selling book The Black Swan. Taleb’s success has stemmed from his focus on highly unlikely events, or samples drawn from far on the tail of a distribution. When such rare samples have a large effect then we have a Black Swan event. These are obviously important in finance, but Taleb also stresses its importance to the progress of science, and here I will sketch a connection to the progress of evolution.

Micro-vs-macro evolution is a purely methodological distinction

On the internet, the terms macroevolution and microevolution (especially together) are usually used primarily in creationist rhetoric. As such, it is usually best to avoid them, especially when talking to non-scientists. The main mistake creationist perpetuate when thinking about micro-vs-macro evolution, is that the two are somehow different and distinct physical processes. This is simply not the case, they are both just evolution. The scientific distinction between the terms, comes not from the physical world around us, but from how we choose to talk about it. When a biologist says “microevolution” or “macroevolution” they are actually signaling what kind of questions they are interested in asking, or what sort of tools they plan on using.

EGT Reading Group 36 – 40, G+ and StackExchange

Around a month and a half ago, I founded an evolutionary game theory Google plus community. Due to my confusion on how G+ works, the community is private and you won’t be able to see any posts until you join. If you have a G+ account then request to join and I will add you to the group. We have several active members that mostly share and comment on new (and sometimes classic) articles. If you don’t have a G+ account then you should make one right away. G+ is much more professional than Facebook or Twitter and much easier to control privacy settings. It is more an interest sharing than general social networking website.

Another community I recommend is StackExchange, which I mentioned previously. Since last year, the Cognitive Sciences SE went live and has been in beta. I’ve been a very active participant (3rd by reputation and voting, and 1st by number of edits) with “The effects of bilingualism on colour perception” as my most popular question (still unanswered) and my most popular answer an explanation of why people subscribe to pseudoscientific theories. Unfortunately, the site is not research level like I had hoped, but it is still a great way to learn and share your knowledge.

If you are a member of SE, or want to make an account, the please follow the up-and-coming Systems Science and Game Theory proposals. It will take a while for those sites to reach an active status, but you can help out by up-voting good questions with fewer than 10 votes or suggesting new ones. Both proposals are extremely relevant to agent-based modeling and game theory.

The final purpose of this post is to celebrate the 40th EGT reading group; I will continue the trend of posting on groups 31-35 and update you on the last five meetings:

2013
March 12	Hauert, C., Holmes, M., & Doebeli, M. [2006] “Evolutionary games and population dynamics: maintenance of cooperation in public goods games.” Proc. R. Soc. B. 273(1600): 2565-2571.
	Hauert, C., Wakano, J.Y., & Doebeli, M. [2008] “Ecological public goods games: cooperation and bifurcation.” Theor. Popul. Biol. 73(2): 257-263.
February 12	Beale, N., Rand, D.G., Battey, H., Croxson, K., May, R.M.,& Nowak, M.A. [2011] “Individual versus systemic risk and the Regulator’s Dilemma.” Proceedings of the National Academy of Sciences, 108(31), 12647-12652.
2012
November 28	Davies, A. P., Watson, R. A., Mills, R., Buckley, C. L., & Noble, J. [2011]. ““If You Can’t Be With the One You Love, Love the One You’re With”: How Individual Habituation of Agent Interactions Improves Global Utility.” Artificial Life, 17(3), 167-181
November 21	Klug, H., & Bonsall, M. B. [2009]. “Life history and the evolution of parental care.” Evolution, 64(3), 823-835.
October 24	Antal, T., Traulsen, A., Ohtsuki, H., Tarnita, C.E., & Nowak, M.A. [2009] “Mutation-selection equilibrium in games with multiple strategies.” Journal of Theoretical Biology 258(4): 614-622.
	Antal, T., Nowak, M.A., & Traulsen, A. [2009] “Strategy abundance in games for arbitrary mutation rates.” Journal of Theoretical Biology, 257 (2), 340-344.

The meetings have been sporadic, but very informative. For three of them I brought guest presenters: Kyler Brown (University of Chicago) for EGT37, Peter Helfer for EGT38, and Yunjun Yang (University of Waterloo) for EGT39. i owe a big thanks to the guys for presenting! If you would like to receive email updates whenever we read a new paper then please contact me (by email or the comments of this post) and I will add you to the list. If you are in Montreal and want to attend or present then you are also welcome to!

Testing for asymptotes and stability

“When should I stop my simulation?” is one of the basic questions that comes up frequently when working with simulations. The question is especially relevant when you are running hundreds or thousands of trials. If the parameter settings are well understood, then sometimes you might have an intuition or analytic reason for not needing to look past a certain length of runs. However, when the point of your work is to understand the parameter space, then you often don’t have this luxury.

I first came across this problem in 2010 when working on my paper “Robustness of ethnocentrism to changes in inter-personal interactions” [pdf, slides] for Complex Adaptive Systems – AAAI Fall Symposium. Since I was looking at the whole space of two-player two-strategy games, there was a huge variability in the system dynamics. In particular, the end of transient behavior of pre-saturated world and the onset of a stable behavior in the post-saturated world varied with the parameters. Since I was up against a deadline, I did not worry too much about this issue, ran my simulations for 3000 time steps, and hoped that the transient behavior was over by that time (it was from a visual inspection of the results after collecting them). Last year, in starting to think about the journal version of the paper, I realized that I should think more carefully about how to test for when I should running my simulations while I am running them.

I quickly realized that the question applies to a much broader setting than my specific simulations. A good algorithm or sound heuristic for this problem could be used in all kinds of simulation settings. Of particular appeal would be a less ad-hoc neuron recruitment criteria for cascade-correlation neural networks or general stopping condition for learning algorithms. Hoping for a quick, simple, and analytically sound solution for this problem, I asked it on the cross validated and, more recently, computational sciences stackexchanges. I also discussed it with Tom Shultz in hopes of insights from exiting stopping criteria in neural net literature. Unfortunately, there does not seem to be a simple answer to this, and most of the current algorithms use very naive and ad-hoc techniques. Since my statistics knowledge is limited, Tom decided to run this question past the quantitative psychologists at McGill. Tom and I will be presenting the question to them this Thursday.

General question

The question can be stated either in terms of time-series or dynamic systems, and I state it in both ways on the two stackexchanges. Since I understand very little about statistics, I prefer the dynamic systems version. I also think this version makes more sense to folks that run simulations, and my original application.

When working with simulations of dynamical systems and I often track a single parameter , such as the number of agents (for agents based models) or the error rate (for neural networks). This parameter usually has some interesting transient behavior. In my agent based models it corresponds to the initial competition in the pre-saturated world, and in neural networks it corresponds to learning. The type and length of this behavior depends on the random seed and simulation parameters. However, after the initial transient period, the system stabilizes and has small (in comparison to the size of the changes in the transient period) thermal fluctuations $\sigma$ around some mean value $x^*$. This mean value, and the size of thermal fluctuations depends on the simulation parameters, but not on the random seed, and are not known ahead of time. I call this the stable state (or maybe more accurately the stochastic stable state) and Tom likes to call it the asymptote.

The goal is to have a good way to automatically stop the simulation once it has transitioned from the initial transient period to the stable state. We know that this transition will only happen once, and the transient period will have much more volatile behavior than the stable state.

Naive approach

The naive approach that first poped into my mind (which I have also seen used as win conditions for some neural networks, for instance) is to pick to parameters 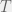and 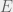, then if for the last 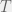timesteps there are not two points and such that 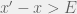then we conclude we have stabilized. This approach is easy, but not very rigorous. It also forces me to guess at what good values of 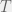and 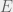should be. It is not obvious that guessing these two values well is any easier than simply guessing the stop time (like I did in my lazy approach by guessing a stop time of 3000 time steps).

After a little though, I was able to improve this naive approach slightly. We can use a time 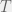and confidence parameter and assume a normal distribution on the error. This will save us the effort of knowing the size of thermal fluctuations.

Let be the change in the time series between timestep 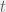and . When the series is stable around 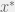, will fluctuate around zero with some standard error. Take the last 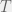, 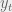‘s and fit a Gaussian with confidence using a function like Matlab’s normfit. The fit will give us a mean with confidence error on the mean 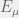and a standard deviation with corresponding error . If 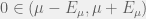, then you can accept. If you want to be extra sure, then you can also renormalize the 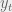s by the you found (so that you now have standard deviation 1) and test with the [Kolmogorov-Smirnov](http://www.mathworks.com/help/toolbox/stats/kstest.html) test at the confidence level, or one of the other strategies in this question.

Although the confidence level is an acceptable parameter, the window size is still a problem. I think this naive approach can be further refined by doing some sort of discounting of past events and looking at the whole history (instead of just the last 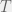timesteps). This would eliminate the need for 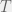but include a discounting scheme as a parameter. If we assume standard geometric discounting, this would not be too bad, but there is no reason to believe that this is a reasonable approach. Further, in the geometric approach the discounting factor will implicitly set a timescale and thus the parameter will be as hard to guess as T. The only advantage is that in this approach everything starts to look like machine learning. Maybe there is a known optimal discounting scheme, or at least some literature on good discounting schemes.

Auto-correlations and co-integration

A slightly more complicated approach proposed by some respondents is auto-correlation and co-integration. The basic idea of both is to look back at your time-series and consider how much it resembles itself. The idea is that the transient period will not resemble itself, and the stable state will not resemble the transient period, however the stable state will resemble itself. Thus, you should detect it via this methods. Unfortunately, they require more complicated tests and are still stuck with a rolling window parameter $T$. Thus, I do not understand their appeal over the refined naive approach.

Testing for structural change

This seems to be the approach by heavy-weight statistics. Unfortunately, I do not have a sufficient stats background to really judge the general suggestion on structural change or the change in error answer. However, there seems to be a statistics literature on detecting structural change. Testing for asymptotes and stability should fall within this literature, but I do not have a good grasp of it and hope that I will gain insights from comments on this post and the presentation on Thursday. For now, I just know that I should be looking closely at the Cross Validated tags on structural-change and change-point. Unfortunately, to detect change points it seems that I need to have a good statistical model of the process that is generating my time-series. Which brings us to the last “answer”: I am not specifying my model with enough detail.

Transient and stable states are ill-defined

In an answer on scicomp, David Ketcheson points out that I do not supply a clear enough definition of transient and stable behavior. The easiest way to see my lack of clear definition is that even if I was offered several tools for detecting asymptotes and stability, I don’t have a criteria to decide which tool is best. I have been suspecting that it would come down to this, and unfortunately have been a bad computer scientists and have not hunkered down to make a general formal model for asking my question. If no better alternatives are suggested on Thursday or in the comments, then I will start to model my system as a POMDP with one strongly connected component that starts somewhere outside this component and eventually decays into it.

The moral of the story: statistics does not magically solve all problems.

Stackexchange and the end of stagnation

For the last 3 months the blog has been stagnant, but this week we resume posting. It was hard to get a reading group started completely online, so we will start holding an official in-person reading group every week at McGill and making a blog post after each one. Hopefully this will provide the critical mass of review posts we need to keep this blog going.

In the meantime, I would like to direct readers to another invaluable tool: the stackexchange network. This is a family of sites descendant from stackoverflow. It is a series of question and answer sites classified by topic. Some of these sites are research level, and others are for beginners and researchers alike. I would like to outline some that might be relevant to people interested in evolutionary game theory:

Theoretical Computer Science is devoted to research level question in theoretical computer science, and the stackexchange site I am most active on. Most questions deal with standard TCS such as algorithm and complexity classes, but EGT, neural networks, genetic algorithms, dynamic systems, and cognition questions sneak in at times. Theoretical physics is the other exclusively research level stackexchange site. I am less familiar with this community (although many of them come from cstheory.SE), and so far have only asked one question about dynamic processes on graphs of the sort we encounter in EGT.

The rest of the stackexchange network allows questions at all levels. Of these I think Biology, Computational Science, Economics, Linguistics, Math, and Stats would be most useful to our readers. These communities are a bit harder to follow, since most questions are not of interest to researchers. However, it is still possible to get useful answers or discussions on the sites. Some of the sites (like Biology) are also early enough in their progress to still be affected by the efforts of a few to steer them towards being research level.

However, our best chance of building a research-level site is to commit to the Cognitive Science proposal. This site is less than 10 users away from going live, and by committing now you will be able to shape its content in the early days of the private beta. Please join and help create an online community for Cognitive Scientists!