Space and stochasticity in evolutionary games

Two of my goals for TheEGG this year are to expand the line up of contributors and to extend the blog into a publicly accessible venue for active debate about preliminary, in-progress, and published projects; a window into the everyday challenges and miracles of research. Toward the first goal, we have new contributions from Jill Gallaher late last year and Alexander Yartsev this year with more posts taking shape as drafts from Alex, Marcel Montrey, Dan Nichol, Sergio Graziosi, Milo Johnson, and others. For the second goal, we have an exciting debate unfolding that was started when my overview of Archetti (2013,2014) prompted an objection from Philip Gerlee in the comments and Philipp Altrock on twitter. Subsequently, Philip and Philipp combined their objections into a guest post that begat an exciting comment thread with thoughtful discussion between David Basanta, Robert Vander Velde, Marc Harper, and Philip. Last Thursday, I wrote about how my on-going project with Robert, David, and Jacob Scott is expanding on Archetti’s work and was surprised to learn that Philip has responded on twitter with the same criticism as before. I was a little flabbergast by this because I thought that I had already addressed Philip’s critique in my original comment response and that he was reiterating the same exact text in his guest post simply for completeness and record, not because he thought it was still a fool-proof objection.

My biggest concern now is the possibility that Philip and I are talking past each other instead of engaging in a mutually beneficial dialogue. As such, I will use this post to restate (my understand of the relevant parts of) Philip and Philipp’s argument and extend it further, providing a massive bibliography for readers interested in delving deeper into this. In a future post, I will offer a more careful statement of my response. Hopefully Philip or other readers will clarify any misunderstandings or misrepresentations in my summary or extension. Since this discussion started in the context of mathematical oncology, I will occasionally reference cancer, but the primary point at issue is one that should be of interest to all evolutionary game theorists (maybe even most mathematical modelers): the model complexity versus simplicity tension that arises from the stochastic to deterministic transition and the discrete to continuous transition.

Stem cells, branching processes and stochasticity in cancer

When you were born, you probably had 270 bones in your body. Unless you’ve experienced some very drastic traumas, and assuming that you are fully grown, then you probably have 206 bones now. Much like the number and types of internal organs, we can call this question of science solved. Unfortunately, it isn’t always helpful to think of you as made of bones and other organs. For medical purposes, it is often better to think of you as made of cells. It becomes natural to ask how many cells you are made of, and then maybe classify them into cell types. Of course, you wouldn’t expect this number to be as static as the number of bones or organs, as individual cells constantly die and are replaced, but you’d expect the approximate number to be relatively constant. Thus number is surprisingly difficult to measure, and our best current estimate is around (Bianconi et al., 2013).

Both 206 and are just numbers, but to a modeler they suggest a very important distinction over which tools we should use. Suppose that my bones and cells randomly popped in and out of existence without about equal probability (thus keeping the average number constant). In that case I wouldn’t expect to see exactly 206 bones, or exactly 37200000000000 cells; if I do a quick back-of-the-envelope calculation then I’d expect to see somewhere between 191 and 220 bones, and between 37199994000000 and 37200006000000. Unsurprisingly, the variance in the number of bones is only around 29 bones, while the number of cells varies by around 12 million. However, in terms of the percentage, I have 14% variance for the bones and only 0.00003% variance in the cell count. This means that in terms of dynamic models, I would be perfectly happy to model the cell population by their average, since the stochastic fluctuations are irrelevant, but — for the bones — a 14% fluctuation is noticeable so I would need to worry about the individual bones (and we do; we even give them names!) instead of approximating them by an average. The small numbers would be a case of when results can depend heavily on if one picks a discrete or continuous model.

In ecology, evolution, and cancer, we are often dealing with huge populations closer to the number of cells than the number of bones. In this case, it is common practice to keep track of the averages and not worry too much about the stochastic fluctuations. A standard example of this is replicator dynamics — a deterministic differential equation governing the dynamics of average population sizes. However, this is not always a reasonable assumption. Some special cell-types, like stem cells, are often found in very low quantities in any given tissue but are of central importance to cancer progression. When we are modeling such low quantities — just like in the cartoon example of disappearing bones — it becomes to explicitly track the stochastic effects — although we don’t have to necessarily name each stem cell. In these cases we switch to using modeling techniques like branching processes. I want to use this post to highlight the many great examples of branching processes based models that we saw at the MBI Workshop on the Ecology and Evolution of Cancer.

Simplifying models of stem-cell dynamics in chronic myeloid leukemia

If I had to identify one then my main allergy would be bloated models. Although I am happy to play with complicated insilications, if we are looking at heuristics where the exact physical basis of the model is not established then I prefer to build the simpleast possible model that is capable of producing the sort of results we need. In particular, I am often skeptical of agent based models because they are simple to build, but it is also deceptively easy to have the results depend on an arbitrary data-independent modeling decision — the curse of computing. Therefore, as soon as I saw the agent-based models for the effect of imatinib on stem-cells in chronic myeloid leukemia (Roeder et al., 2002; 2006; Horn et al., 2013 — the basic model is pictured above), I was overcome with the urge to replace it by a simpler system of differential equations.

Evolutionary games in finite inviscid populations

Last week, we saw how to deal with two-strategy games in finite inviscid populations. Unfortunately, two strategy games are not adequate to model many of the interactions we might be interested in. In particular, we cannot use Antal et al. (2009a) to look at bifurcations and finitary/stochastic effects in tag-based models of ethnocentrism, at least not without some subtle tricks. In this post we are going to look at a more general approach for any -strategy game developed by Antal et al. (2009b). We will apply these tools to look at a new problem for the paper, but an old problem for the blog: ethnocentrism.

Antal et al. (2009b) consider a large but finite population of size 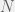and a game with strategies. For update rule, they focus on the frequency dependent Moran process, although their results also hold for Wright-Fisher, and pairwise comparison (Fermi rule). Unlike the previous results for two-strategy games, the present work is applicable only in the limit of weak selection. Mutations are assumed to be uniform with probability : a mutant is any one of the strategies with equal probabilities. However, in section 4.2, the authors provide a cute argument for approximating non-uniform but parent-independent mutation rates by repeating strategies in proportion to the likelihood of mutation into them. Much like the two-strategy case, the authors derive separate equations for low and high mutation rates, and then provide a way to interpolate between the two extremes for intermediate mutation rates.

The mathematics proceeds through a perturbation analysis. The basic idea is to solve for the distribution of strategies in the drift (no selection) model, and then to gradually dial up the selection to perturb the distribution slightly into the weak selection regime. The authors use this to arrive at the following to conditions for low, and high mutation for strategy 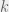to be favored:

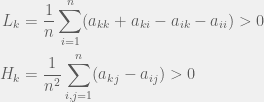
There is an intuitive story to help understand these two conditions. In the case of low mutation, the population is usually just two strategies until one of them fixes. So for the terms that matter are the pairwise interactions between the strategies, and since the most decisive (and entropy rich) case is near the 50-50 split in the two strategies, self interactions () and other-strategy interactions () happen with the same frequency. I think this is where the discrepancy with Antal et. al (2009a) that we will see later sneaks in. A correction factor of should be added in front of the the self-interaction terms, but I digress.

For the high mutation case, all the strategies are present in the population with about the same frequency at the same time. We need to look at the transitions from this population to get our first order terms. In that case, the focal individual’s fitness is (since all opponents are equally likely; once again, I believe a correction term is in order), and the average fitness is . The difference of these two terms produces .

In order to interpolate, we have the following condition for strategy 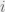to be more common than for intermediate mutation rates :

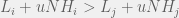
How does this disagree with the two-strategy results of Antal et al. (2009a)? The present paper reproduces the condition of risk-dominance, with C dominating D if 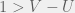, but does not produce the small 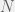correction of . This would be mitigated with the observations I made earlier, but the approach of the perturbation analysis would have to be modified carefully.

The perturbation method can be extended to mixed strategies, as is done by Tarnita et al. (2009). In that case, we just replace the summation by integrals, to get:

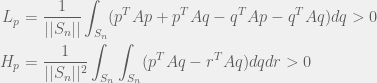
Where 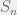is the n-vertex simplex with volume . It is nice to know that the results generalize to mixed strategies, but not as important tool as the pure strategy variant. I will concentrate on pure strategies, although mixed might be good to revisit to study evolution of agency.

Antal et al. (2009b) showcase their method with three case studies: (i) cooperators, defectors, and loners, (ii) reversing the rank of strategies by mutation, and (iii) cooperators, defectors, and tit-for-tat. The first is the most interesting for me, since it shows how adding an irrelevant strategy, can reverse the dominance of the other two. I will present their example in a more general context for all cooperate-defect games. We will introduce an irrelevant strategy L, where irrelevance means that both C and D get the same payoff 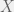from interacting with L and L gets 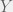from them. The self interaction payoff for L can differ, and we can set it to :

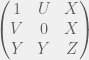
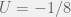The authors consider the particular case of and , and . We can apply the general results to get (for small mutations):

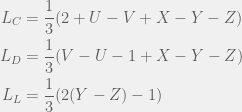
We can look at at the condition for C to dominate D for small mutations () to get . If we had used 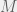different irrelevant strategies (or just dialed up the proportion of mutations to an irrelevant strategy) then would be replaced by . This creates a new strip of cooperation which reaches into the Prisoner’s dilemma region (drawn in blue):

When we switch to large mutations, the region disappears and we recover the standard 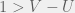rule. Note that this example means that, for this analysis, we cannot ignore competing strategies even if they are strictly dominated.

Ethnocentrism in tag-based models

We will consider a strategy space of tags, with an agent of each tag being either a humanitarian (cooperate with all), ethnocentric (cooperate with same-tag), traitorous (cooperate with oot-tags), or selfish. For the game, we will look at the usual cost-benefit representation of Prisoner’s dilemma. Note that the and 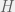values will be the withing a single strategy of different tags, so we only need to compute four of each:

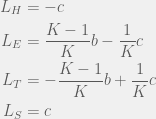
This divides the dynamics into two regions, w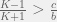hen then , otherwise we have . In other words, for large enough or small enough , ethnocentrism can be the dominant strategy in the population. This condition is in perfect agreement with the Traulsen & Nowak (2007) results we saw earlier. Although in that case, there were no H or T agents. If we remove H & T from the current analysis, we will still get the same condition for ethnocentric dominance even though we will calculate different values.

For large mutations, the advantage of ethnocentrics disappears completely, and we get:

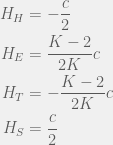
Which for results in the ordering 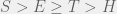. So if we have mutations that change tag and strategy together (as they do in this case) then higher mutation rates disadvantage the population, and if we let be the expected number of mutants per generation, then we can see that ethnocentric cooperation is possible only if or rewritten as .

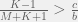References

Antal, T., Nowak, M.A., & Traulsen, A. (2009a). Strategy abundance in games for arbitrary mutation rates Journal of Theoretical Biology, 257 (2), 340-344.

Antal T, Traulsen A, Ohtsuki H, Tarnita CE, & Nowak MA (2009b). Mutation-selection equilibrium in games with multiple strategies. Journal of Theoretical Biology, 258 (4), 614-22 PMID: 19248791

Tarnita, C.E., Antal, T., Nowak, M.A. (2009) Mutation-selection equilibrium in games with mixed strategies. Journal of Theoretical Biology 26(1): 50-57.

Traulsen A, & Nowak MA (2007). Chromodynamics of cooperation in finite populations. PLoS One, 2 (3).

Risk-dominance and a general evolutionary rule in finite populations

In coordination games, the players have to choose between two possible strategies, and their goal is to coordinate their choice without communication. In a classic game theory setting, coordination games are the prototypical setting for discussing the problem of equilibrium selection: if a game has more than one equilibrium then how do the players know which one to equilibrate on? The standard solution concept for this is the idea of a risk dominance. If you were playing a symmetric coordination game:

where and , then how would you chose your strategy not knowing what your opponent is going to do? Since the two pure strategy Nash equilibria are the top left and bottom right corner, you would know that you want to end up coordinating with your partner. However, given no means to do so, you could assume that your partner is going to pick one of the two strategies at random. In this case, you would want to maximize your expected payoff. Assuming that each strategy of your parner is equally probably, simple arithmetic would lead you to conclude that you should chose the first strategy (first row, call it C) given the condition:

Congratulations, through your reasoning you have arrived at the idea of a risk dominant strategy. If the above equation is satisfied then C is risk dominant over D (the second strategy choice), more likely to be selected, and the ‘better’ Nash equilibrium.

Since many view evolutionary game theory as a study of equilibrium selection, it is not surprising to see risk-dominance appear in evolution. In particular, if the risk dominance condition is met, then (for a coordination game and replicator dynamics) C will have a larger basin of attraction than D. If we pick initial levels of cooperators at random, then in your well-mixed and extremely large population, the risk-dominant strategy will dominate the population more often. If you are feeling adventurous, then I recommend as exercise to calculate the exact probability of C dominating in this setting.

From our experience with ethnocentrism and discrete populations, we know that replicator dynamics is not the end of the story. The second step is to consider finite inviscid populations where we can’t ignore dynamical stochasticity. Kandari et al. (1993) studies this setting and for a population of size concluded that C would be a more likely than D if:

Nowak et al. (2004) looked at this problem from the biological perspective of Moran processes. In a Moran process, there is no mutation, and thus the conclusion of dynamics is the absorbing state of either all C or all D. The quantity of interest becomes the fixation probability: the fixation probability of C is the probability that a single C mutant invades (leads to an all C absorbing state) a population of all D (vice-virsa for
fixation of D). Nowak et al. (2004) found that the fixation probability of C (in the weak selection limit) is higher than that of D in a population of agents if and only if the above equation is satisfied.

Antal et al. (2009) concluded this research program. They showed that the above condition was necessary for the case of arbitrary mutations, a wide range of evolutionary processes, and any two player, two strategy game. It is true for pair-comparison (Fermi rule), exponential Moran processes, and weak-selection Moral processes with arbitrary mutation rates. In general, any update process that satisfies the two requirements: (i) additive payoffs, and (ii) evolutionary dynamics depend only on the payoff differences.

Let us visualize this result. As we learnt in a previous post we know that a two strategy cooperate-defect games do not need 4 parameters to specify, and can be rewritten with just two. The symmetry arguments we applied before preserve the authors’ result, so let’s apply the transformation:

This lets us simplify the risk-dominance and finite population rules to:

Now it clear why we discussed risk-dominance before diving into finite populations. As the population size gets arbitrarily large (), our finite population rule reduces to risk-dominance and replicator dynamics. In the other extreme case is (can’t have a game with smaller populations) the rule becomes .

In the above picture of U-V space, we can see the two extreme conditions. In the green region, C is more likely than D for any population size, and in the blue it is true in the limit of infinite population. For particular you get a different division line in the blue region parallel to the two current ones. Give a specific game in the blue region, you can calculate the threshold:

For games in the blue region, if your population exceeds the threshold then C with be more likely than D.

For those interested in the mathematical details, I recommend sections 2.3 and 4 of Antal et al. (2009). In particular, I enjoy their approach in section 2.3 of showing that when the game is on the dividing line then we have a symmetric distribution around and due to the well-behaved nature of deformations of the game matrix we can extend to the non knife-edge case. The only missing study in Antal et al. (2009) is a study of the second moment of the population. In regions 5, 9, and 10 we expect a bimodal distribution, and in 2-4 and 6-8 a unimodal. Can we use the probability of mutation to bound the distance between the peaks in the former, and the variance of the peak in the latter? Another exercise for the highly enthusiastic reader.

References

Antal, T., Nowak, M.A., & Traulsen, A. (2009). Strategy abundance in games for arbitrary mutation rates Journal of Theoretical Biology, 257 (2), 340-344 DOI: 10.1016/j.jtbi.2008.11.023

Kandori, M., Mailath, G.J., & Rob, R. (1993). Learning, mutation, and long run equilibria in games. Econometrica 61(1): 29-56.

Nowak, M.A., Sasak, A., Taylor, C., & Fudenberg, D. (2004). Emergence of cooperation and evolutionary stability in finite populations. Nature 428: 646-650.

How would Alan Turing develop biology?

Alan M. Turing (23 June 1912 – 9 June 1954)
photo taken on March 29th, 1951.

Alan Turing was born 100 years ago, today: June 23rd, 1912. He was a pioneer of computing, cryptography, artificial intelligence, and biology. His most influential work was launching computer science by the definition of computable, introduction of Turing-machine, and solution of the Entscheidungsproblem (Turing, 1936). He served his King and Country in WW2 as the leader of Hut 8 in the Government Code and Cypher School at Bletchley Park. With his genius the British were able to build a semi-automated system for cracking the Enigma machine used for German encryption. After the war he foresaw the connectionist-movement of Cognitive Science by developing his B-type neural network in 1948. He launched the field of artificial intelligence with Computing machinery and intelligence (1950), introducing the still discussed Turing test. In 1952 he published his most cited work: The Chemical Basis of Morphogenesis spurring the development of mathematical biology. Unfortunately, Turing did not leave to see his impact on biology.

In 1952, homosexuality was illegal in the United Kingdom and Turing’s sexual orientation was criminally prosecuted. As an alternative to prison he accepted chemical castration (treatement with female hormones). On June 8th, 1954, just two weeks shy of his 42nd birthday, Alan Turing was found dead in his apartment. He died of cyanide poisoning, and an inquire ruled the death a suicide. A visionary pioneer was taken and we can only wonder: how would Alan Turing develop biology?

In The Chemical Basis of Morphogenesis (1952) Turing asked: how does a spherically symmetric embryo develop into a non-spherically symmetric organism under the action of symmetry-preserving chemical diffusion of morphogens? Morphogens are abstract particles that Turing defined; they can stand in place for any molecules relevant to developmental biology. The key insight that Turing made is that very small stochastic fluctuations in the chemical distribution can be amplified by diffusion to produce stable patterns that break the spherical symmetry. These asymmetric patters are stable and can be time-independent (except a slow increase in intensity), although with three or more morphogens there is also the potential for time-varying patterns.

The beauty of Turing’s work was in its abstraction and simplicity. He modeled the question generally via Chemical diffusion equations and instantiated his model by considering specific arrangements of cells like a discrete cycle, and a continuous ring of tissue. He proved results that were general and qualitative in nature. On more complicated models he also encouraged a numeric quantitative approach to be carried out on the computer he helped develop. It is these rigorous qualitative statements that have become the bread-and-butter of theoretical computer science (TCS).

For me, rigorous qualitative statements (valid for various constants and parameters) instead of quantitative statements based on specific (in some fields: potentially impossible to measure) constant and parameters is one of the two things that sets TCS apart from theoretical physics. The other key feature is that TCS deals with discrete objects of arbitrarily large size, while (classical) physics assumes that the relevant behavior can be approximated by continuous variables. The differential equation approach of physics can provide useful approximations such as replicator dynamics (example applications: perception-deception and cost-of-agency), I think it is fundamentally limited. Differential equations should only be used for intuition in fields like theoretical biology. Although Turing did not get a chance to pursue this avenue, I think that he would have pushed biology into the direction of using more discrete models.

Shnerb et al. (2000) make a good point for the importance of discrete models. The model is of spatial diffusion with two populations: catalyst A that never expires and a population B — agents of which expire at a constant rate and use A to catalyze reproduction. The authors use the standard mean-field diffusion approach to look at the parameter range where the abundance of A is not high enough to counteract the death rate of B agents. The macro-dynamic differential equation approach predicts extinction of the B-population at an exponential rate. However, when the model is simulated at micro-dynamic level with discrete agents, then there is no extinction. Clumps of B agents form and follow individual A agents as they follow Brownian motion through the population. The result is an abundance of life (B agents) at the macro-scale in contrast to the continuous approximation. This is beautifully summarized by Shnerb et al. (2000) in the figure below.

Figure 1 from Shnerb et al. (2000) showing Log of B agent concentration versus time for discrete (solid blue line) and continues (dotted red line) models.

Like Turing’s (1952) approach, the discrete model also shows clumping and symmetry breaking. However, the requirements are not as demanding as what Turing developed. Thus, it is natural to expect that Turing would have found similar models if he continued his work on morphogenesis. This is made more likely by Turing’s exploration of discrete computer models of Artificial Life prior to his death. I think that he would have developed biology by promoting the approach of theoretical computer science: simple abstract models that lead to rigorous qualitative results about discrete structures; Alan Turing would view biology through algorithmic lenses. Since he is no longer with us, I hope that myself and others can carry on his vision.

References

Shnerb NM, Louzoun Y, Bettelheim E, & Solomon S (2000). The importance of being discrete: Life always wins on the surface. Proceedings of the National Academy of Sciences of the United States of America, 97 (19), 10322-4 PMID: 10962027

Turing, A. M. (1936). On Computable Numbers, with an Application to the Entscheidungsproblem. Proceedings of the London Mathematical Society 2(42): 230–65.

Turing, A. M. (1950) Computing Machinery and Intelligence. Mind.

Turing, A. M. (1952). The Chemical Basis of Morphogenesis. Philosophical Transactions of the Royal Society of London 237 (641): 37–72. DOI:10.1098/rstb.1952.0012