Bifurcation of cooperation and inviscid ethnocentrism
June 26, 2012 12 Comments
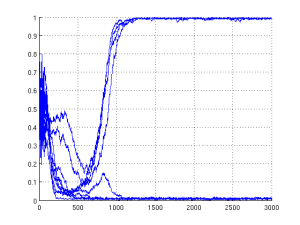
Proportion of cooperation versus evolutionary cycle in an inviscid variant of the H&A model with 4 tags and a competitive (c/b = 0.8) environment. The graph shows 10 simulations, with each run represented by its own line
I was fooling around with my ethnocentrism code and testing various game parametrizations and treatments of viscosity. I was too lazy to generate my standard average plots and so I followed a technique I have seen in biology: plotting all the runs as separate lines on one plot. The result is to the right of this paragraph.
Each run is represented by a blue line. The strange phenomena is the clear bifurcation in cooperation shortly after world saturation (which typically occurs close to the 500th cycle for these parameters). One can clearly see that four of the simulations resulted in complete cooperation, and six in total defection. Having such a sharp bifurcation is already surprising, but what makes this graph truly astonishing is that the environment is inviscid. The agents interact with their 4 neighbours, but their children are placed randomly into the lattice. Children do not reside close to their parents, and yet we see cooperation.
This is in direct opposition to my paper with with Tom: “Ethnocentrism Maintains Cooperation, but Keeping One’s Children Close Fuels It” (Kaznatcheev & Shultz, 2011). We had concluded that local child-placement — also known as viscosity — was essential for cooperation; tags only factored in after world saturation as a mechanism to maintain cooperative interactions. The figure also seems contrary to the inviscid variants results in Hammond & Axelrod (2006) that they used to support their use of a spatial structure. Most importantly, it disagrees with the approximation by replicator equation! Is discreteness doing something critical here? Most importantly, how did we miss this?!

Proportion of cooperation versus evolutionary cycle for four different conditions. In blue is the standard H&A model; green preserves local child placement but eliminates tags; yellow (the case of interest) has tags but no local child placement; red is both inviscid and tag-less. The lines are from averaging 30 simulations for each condition, and thickness represents standard error. Figure appeared in Kaznatcheev & Shultz (2011); the black circle, horizontal bars, and arrow have been added for this post.
A tell-tale sign of the result was hiding in our graphs (one of them is reproduced above). I have annotated the graph for easier viewing. Note how thick the line is inside the black circle. This means there is a great amount of variance between simulation runs, and I should have taken the time to look at them individually. Towards the end of the 1000 cycles, there is also a significant rise in the amount of cooperation — I should have run the simulations longer to gather more complete data. These hints give away that there might be something strange happening, why were they ignored? Mostly because this was an extreme case (a very noncompetitive environment c/b = 0.25; cooperation should be easy) and the more interesting case (c/b = 0.5) was much more definitive and did not show either artifact.
An ideal situation would be to go back to the raw data and reanalyze it more carefully. However, these simulations were run in the summer of 2008 and the files are locked away on some distant external hard-drive. Most importantly, the model has evolved slightly in the years since and is in a more refined state. I simply ran new simulations with parameters approximating the early work as closely as I could. The results are dramatic.

Proportion of cooperation versus evolutionary cycle of 30 simulations run for 3000 cycles. Runs that had less than 5% cooperation (13 runs) in the last 500 cycles are traced by red lines; more than 95% cooperation (9 runs) by green; intermittent amounts (8 runs) are yellow. The black line represents the average of all 30 runs, no standard error is shown.
We see five different regimes. A simulation either goes towards all cooperation (or all defection) as it reaches world saturation, or it oscillates until it switches to all cooperation (or all defection) or maybe continues indefinitely. I think this last regime is unlikely, and the eight yellow oscillating runs are simply an artifact of not having run the model long enough. How can we calculate a priori for how long to run the model? Can we predict which regime a given world (at saturation) will fall into? Do the oscillations follow a fixed period? Can we predict this period? What model parameters does the period depend on? This one figure gives us so many new questions!

Proportion of cooperation versus evolutionary cycle of the three main categories for the first 1000 cycles. Green are the worlds that ended in cooperation (9 runs); Yellow are the ones still oscillating at 3000 cycles (8 runs); Red are the simulations that ended in defection (13 runs). The black line represents the average of the 30 runs. The thickness of lines is their standard error.
I have fooled around with Fourier analysis on the proportion of cooperation before. However, I’ve never had such nice looking waves to work with; the Fourier transform always turned up noise. I am definitely hopeful that the yellow runs will have some secrets for us. At a quick glance it seems that the magnitude of oscillations is important in determining if the world will go towards cooperation or defection. The bigger oscillations seem to go to defection. I need more data and a careful analysis. For now, I will go back to averaging and look at the three categories I created.
On the left is a figure of averaging across the categories restricted to the first 1000 cycles. The black run on the left seems very similar to the tags and no child proximity run from before, even if they don’t agree numerically. It is clear that at the end of 1000 cycles, the three categories are separating. With a more thorough analysis, I could have noticed these result back in 2008; catching up on lost time!

Proportion of cooperation versus cycle for 30 runs without viscoscity or tags. Individual runs are in red, and the mean in black
These results are made more exciting by the importance of tags. If we remove tags from the simulation then all the interesting behavior disappears! On the right you see 30 simulations with the same exact parameters as before, except tag information is removed (there is only one tag, unlike the four in the previous case). Every run ended in defection and was colored red. A natural question to ask is what is the minimal threshold for number of tags needed to achieve bifurcation. Can we do it with just two? Laird (2011) showed that there is a very specific strangeness associated with two tags that is not present for one, three, or more tags. Thus, it is definitely essential to recreate all of the above with exactly two tags. This two-tag case is manageable for replicator dynamics, so we can compare analytic and simulation predictions directly.
Traulsen & Nowak (2007) and Antal et al. (2009) have already shown that ethnocentrism can evolve without spatial structure. However, their work relies on having an arbitrarily large number of possible tags (or the ability to innovate new tags) and a different mutation rate for transmission of tags and strategy. Neither of these features is present in our model. In other words, a careful analysis of the results might yield new insight into the simplest mechanisms for the evolution of cooperation.
References
Antal, T., Ohtsuki, H., Wakeley, J., Taylor, P.D., & Nowak, M.A. (2009). Evolution of cooperation by phenotypic similarity. Proc Natl Acad Sci U S A. 106(21): 8597–8600.
Hammond, R.A., & Axelrod, R. (2006). Evolution of contingent altruism when cooperation is expensive. Theoretical Population Biology 69(3): 333–338.
Kaznatcheev, A., & Shultz, T.R. (2011). Ethnocentrism Maintains Cooperation, but Keeping One’s Children Close Fuels It. Proceedings of the 33rd Annual Conference of the Cognitive Science Society, 3174-3179
Laird, R.A. (2011). Green-beardeffectpredicts the evolution of traitorousness in the two-tagPrisoner’sdilemma. Journal of Theoretical Biology 288: 84–91.
Traulsen, A., & Nowak, M.A. (2007). Chromodynamics of Cooperation in Finite Populations. PLoS ONE 2(3) e270.
