Is Chaitin proving Darwin with metabiology?
June 29, 2012 27 Comments
Algorithmic information theory (AIT) allows us to study the inherent structure of objects, and qualify some as ‘random’ without reference to a generating distribution. The theory originated when Ray Solomonoff (1960), Andrey Kolmogorov (1965), and Gregory Chaitin (1966) looked at probability, statistics, and information through the algorithmic lens. Now the theory has become a central part of theoretical computer science, and a tool with which we can approach other disciplines. Chaitin uses it to formalize biology.
In 2009, he originated the new field of metabiology, a computation theoretic approach to evolution (Chaitin, 2009). Two months ago, Chaitin published his introduction and defense of the budding field: Proving Darwin: Making Biology Mathematical. His goal is to distill the essence of evolution, formalize it, and provide a mathematical proof that it ‘works’. I am very sympathetic to this goal.
Chaitin’s conviction that evolution can be formalized stems from his deeply Platonic view of the world. Since evolution is so beautiful and ubiquitous, there must be a pure perfect form of it. We have to look past the unnecessary details and extract the essence. For Chaitin this means ignoring everything except the genetic code. The physical form of the organisms is merely a vessel and tool for translating genes into fitness. Although this approach might seem frightening at first, it is not foreign to biologists; Chaitin is simply taking the gene-centered view of evolution.
As for the genetic code, Chaitin takes the second word very seriously; genes are simply software to be transformed into fitness by the hardware that is the physics of the organisms’ environment. The only things that inhabit this formal world are self-delimiting programs — a technical term from AIT meaning that no extension of a valid program is valid. This allows us to define a probability measure over programs written as finite binary strings, which will be necessary in the technical section.
Physics simply runs the programs. If the program halts then the natural number it outputs is the program’s fitness. In other words, we have a perfectly static environment. If you were interested ecology or evolutionary game theory, then Chaitin just threw you out with the bath water. If you were interested in modeling, and wanted to have something computable define your fitness, then tough luck. Finally, in a fundamental biological theory, I would expect fitness to be something we measure when looking at the organisms, not a fundamental quantity inherent in the model. In biology, a creature simply reproduces or doesn’t, survives or doesn’t; fitness is something the observer defines when reasoning about the organisms. Why does Chaitin not derive fitness from more fundamental properties like reproduction and survival?
In Chaitin’s approach there is no reproduction, there is only one organism mutating through time. If you are interested in population biology, or speciation then you can’t look at them in this model. The mutations are not point-mutations, but what Chaitin calls algorithmic mutations. The algorithmic mutation actually combine the act of mutating and selecting into one step, it is a -bit program that takes the current organism A and outputs a new organism B of higher fitness (note, that it needs an oracle call for the Halting-problem to do so). The probability that A is replaced by B is then
. There is no way to decouple the selection step from the mutation step in an algorithmic mutation, although this is not clear without the technical details which I will postpone until a future post. Chaitin’s model does not have random mutations, it has randomized directed mutations. Fitness as a basic assumption, static environment, and directed mutations make this a teleological model — a biologist’s nightmare.
What does Chaitin achieve? His primary result is to show biological creativity, which in this model means a constant (and fast) increase in fitness. His secondary result is to delineate between three types of design: blind search, evolution, and intelligent design. He shows that to arrive at an organism that has the maximum fitness of any -bit organism (this is the number
— the
th busy beaver number), blind search required on the order of
steps, evolution requires between
and
, and intelligent design (that selects the best algorithmic mutation at each step) requires
steps. These are interesting questions, but what do they have to do with Darwin?
Does Chaitin prove Darwin?
We are finally at the central question of this post. To answer this, we need to understand what Darwin achieved. The best approach is to look at Mayr’s (1982) five facts and three inferences that define Darwin’s natural selection:
- Fact 1: Population increases exponentially if all agents got to reproduce.
Metabiology: A single agent that doesn’t reproduce - Fact 2: Population is stable except for occasional fluctuations.
Metabiology: There is always one agent, thus stable - Fact 3: Resources are limited and relatively constant.
Metabiology: Resources are not defined. - Inference 1: There is a fierce competition for survival with only a small fraction of the progeny of each generation making it to the next.
Metabiology: Every successful mutation makes it to the next generation. - Fact 4: No two agents are exactly the same.
Metabiology: There is only one agent. - Fact 5: Much of this variation is heritable.
Metabiology: Nothing is heritable, a new mutant has nothing to do with the previous agent except having a higher fitness. - Inference 2: Survival depends in part on the heredity of the agent.
Metabiology: A mutant is created/survives only if more fit than the focal agent. - Inference 3: Over generations this produces continual gradual change
Metabiology: Agent constantly improves in fitness
The only thing to add to the above list is the method for generation variation: random mutation. As we saw before, metabiology uses directed mutation. From the above, it mostly seems like Chaitin and Darwin were concerned about different things. Chaitin doesn’t prove Darwin.
However, I don’t think Chaitin’s exercise was fruitless. I think it is important to try to formalize the basic essence of evolution, and to prove theorems about it. However, I think Chaitin needs to remember what made his development of algorithmic information theory so successful. AIT was able to address existing questions of interest in novel ways. So the lesson of this post is to concentrate on the questions biologists want to answer (or have answered already) when building a formal model. Make sure that your formal approach can at least express some of the questions a biologist would want to ask.
References
Chaitin, G. (1966). On the Length of Programs for Computing Finite Binary Sequences. J. Association for Computing Machinery 13(4): 547–569.
Chaitin, G. (2009). Evolution of Mutating Software EATCS Bulletin, 97, 157-164
Kolmogorov, A. (1965). Three approaches to the definition of the quantity of information. Problems of Information Transmission 1: 3–11
Mayr, E. (1982). The Growth of Biological Thought. Harvard University Press. ISBN 0-674-36446-5
Solomonoff, R. (1960). A Preliminary Report on a General Theory of Inductive Inference. Technical Report ZTB-138, Zator Company, Cambridge, Mass.


I disagree with your characterization of algorithmic mutations as directed.
They are in fact random.
Rgds,
GJC
As you describe them in chapter 5 they do seem random. However, your precise definition of the mutation operator in appendix 2 cannot create organisms of lower fitness. If then the mutant doesn’t halt and has no well-defined fitness. The only time a mutant is defined is when it has a higher fitness, thus this is a directed mutation. Of course, you pick one of the directed mutations at random, and hence I think algorithmic mutations are randomized directed mutations.
then the mutant doesn’t halt and has no well-defined fitness. The only time a mutant is defined is when it has a higher fitness, thus this is a directed mutation. Of course, you pick one of the directed mutations at random, and hence I think algorithmic mutations are randomized directed mutations.
Maybe I am missing the point completely, though. I tried to provide a more detailed explanation in my new post:
Let me know what I am misunderstanding.
Have you received further comments from Chaitin after your post of July, 8, 2012?
I find your critique quite interesting…
I have not heard from Chaitin, and I don’t plan on contacting him. There are too many good models out there that I’d rather concentrate on learning from.
If you are interested in questions of evolvability from a computer science perspective then I recommend looking at Leslie Valiant’s work (pdf). It suffers from some similar downsides as Chaitin’s (such as a lack of dynamic fitness landscapes), but it uses cstheory in a non-trivial way and makes very interesting connections to machine learning white remaining interesting to a biologist. I have discussed it briefly in a recent post and have been planning to write more extensively on it for some time now.
I think that your review in some ways misses an important point exactly while making it —
in your outline where you describe the difference between Chaitlin’s metabiology and Mayr’s 5 facts, note that for each of the facts, the simplified model provides an upper bound to the complexity. In this upper bound model, random search has exponential complexity while Darwinian evolution and intelligent design have polynomial complexity (quadratic and linear).
–so despite the tone being too self congratulatory and too superficial, I think that the book does “prove Darwin” by showing in a model that by adding selection to random search, the complexity is reduced from exponential to quadratic.With a little hand waiving, it doesn’t take much to believe that the same is the case of more realistic models.
Thanks for the feedback! You make a valid point, but I think there are some limitations to it.
I disagree that it is “an upper bound” model. In particular, Chaitin’s mutations are directed, this allows a speed up because drift is not possible, but that would only make a quadratic difference usually. Most important, though, is that his fitness landscape is extremely simple. In the mathematical biology literature, his landscape would be known as a Mt, Fuji landscape — every shortest path is an adaptive path. It has been known since the late 80s that in this sort of landscape, evolution is exponentially faster than exhaustive search (In fact — and this is another non-general feature of Chaitin, but one that plays in his favor as you pointed out — if you allow larger sexual populations then it can be doubly-exponentially faster as I discuss briefly here). Unfortunately, it has also been known that this is NOT a reasonable fitness landscape model for evolution. With a more realistic landscape model evolution where not every shortest path is adaptive, evolution can slow down a lot. One of my recent research projects for instance, shows that in some realistic (i.e. used by biologists) fitness landscapes, evolution is just as slow (asymptotically) as exhaustive search.
If you were to build a fully general fitness landscape model (i.e. what you would need for an “upper bound model” as you describe) then you would have to allow any landscape. Of course, such a model is boring, since it is trivial to build an example landscape where evolution — or actually any algorithm (except quantum ones, where Grover search allows a quadratic speed up, but that is still just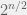 ) — will be as slow as exhaustive search. Simply select one genotype (i.e. string
) — will be as slow as exhaustive search. Simply select one genotype (i.e. string 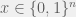 ) to have fitness 1 and all other
) to have fitness 1 and all other 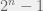 strings to have fitness 0. Now, starting at a random point in this landscape and trying to find the fitness peak is equivalent to searching an unordered list of exponential size For comparison, the Mt. Fuji landscape Chaitin useses corresponds to a sorted list, so it is not surprising that ‘intelligent design’ (i.e. binary search) or ‘evolution’ (i.e. randomized binary search — where we take a step in the right direction, but the size of the step is random instead of exactly to the half-way point) is faster than exhaustive linear search.
strings to have fitness 0. Now, starting at a random point in this landscape and trying to find the fitness peak is equivalent to searching an unordered list of exponential size For comparison, the Mt. Fuji landscape Chaitin useses corresponds to a sorted list, so it is not surprising that ‘intelligent design’ (i.e. binary search) or ‘evolution’ (i.e. randomized binary search — where we take a step in the right direction, but the size of the step is random instead of exactly to the half-way point) is faster than exhaustive linear search.
It is easy to see from the get-go that Chaitin’s model will be unsatisfying. A satisfying model will be one where for some “types of landscapes” evolution is faster that blind search and for some it is slower, and we have some empirical test to check which ones correspond to the one we live in. In this way, Valiant’s machine learning approach (discussed briefly here) is much more interesting. It gives some examples where evolution is possible in polytime and others where it is not. Any interesting result in this field would have to have that sort of structure.
P.S. Comments on the blog can only be nested to a certain depth, so please start a new thread. You don’t have to respond to a previous comment of mine directly since as the author of this post, I will be notified of all comments. Thank you for your discussion :D.
in response to your comment August 15, 2013 at 22:28
Thanks for the interesting clarification! I will follow-up on your leads as I have time.
Best Regards,
-gi
I am glad to be helpful. I have expanded on this theme in my most recent post. Although it only address Chaitin’s work in passing, I talk about fitness landscapes extensively so it might help make your follow-up more enjoyable.
Pingback: Critique of Chaitin’s algorithmic mutation « Theory, Evolution, and Games Group
Pingback: Is Chaitin proving Darwin with metabiology? | Social Foraging | Scoop.it
Pingback: Is Chaitin proving Darwin with metabiology? | Mind Candy { interdimensionally } Cubed... It's SO yesterday to be a Square | Scoop.it
Quite similar to Melanie Mitchell’s Genetic Algorithms – in fact one sees many of the same principles laid out. Applications by Adami and others have had similar results, good luck in your results.
I don’t see the similarity. Adami’s work is of interest to actual biologists, and tries to capture aspects of evolution as it is treated in ecology and biology, Chaitin doesn’t connect to biology at all.
General work on genetic algorithms produces potentially useful optimization technique, while Chaitin’s ideas cannot be hijacked for such uses. However, genetic algorithms are pretty difficult to analyze: http://cstheory.stackexchange.com/q/844/1037
Pingback: Is Chaitin proving Darwin with metabiology? | Science, I choose you! | Scoop.it
Pingback: Some stats on the first 50 posts « Theory, Evolution, and Games Group
Pingback: Interdisciplinitis: Do entropic forces cause adaptive behavior? | Theory, Evolution, and Games Group
Pingback: Micro-vs-macro evolution is a purely methodological distinction | Theory, Evolution, and Games Group
Pingback: Stats 101: an update on readership | Theory, Evolution, and Games Group
Pingback: Fitness landscapes as mental and mathematical models of evolution | Theory, Evolution, and Games Group
Pingback: Cataloging a year of blogging: the algorithmic world | Theory, Evolution, and Games Group
Pingback: Kooky history of the quantum mind | Theory, Evolution, and Games Group
Pingback: Evolution is a special kind of (machine) learning | Theory, Evolution, and Games Group
Pingback: Why academics should blog and an update on readership | Theory, Evolution, and Games Group
Pingback: Evolution News & Views
Very interesting critique Artem! Thank you for writing it.
I had a question, and please forgive me if I misunderstand anything:
When you say:
“Fact 5: Much of this variation is heritable.
Metabiology: Nothing is heritable, a new mutant has nothing to do with the previous agent except having a higher fitness.”
Can I ask what may well be a silly question:
– If the new mutant in Chaitin’s model has *any* characteristics that are the same as the old agent, wouldn’t that – functionally – be a case of heritability/inheritance of characteristic/s?
Chaitin says (p60)
“So that’s my fitness measure. Each of my software organisms calculates a bigger number, and the bigger the number, the fitter the organism.” (Chaitin 2013 p. 60)
This means there is at least one parameter remaining constant: numbers.
(Alternatively if Chaitin’s algorithm created a new symbolic form each time, eg 1. alpha-numeric characters; 2. pictograms 3. Euclidean geometrical shapes, 4. Non-Euclidean goemetrical shapes 5. A colour 6. An n-dimensional object 7. A novel (like in the library of Borges etc) 8. Some random other thing, etc) then yes there would be no heritability, but: they are all numbers he is generating and then testing for comparative fitness (relative to, the previous number).
So, isn’t there heritability?
There is obviously natural selection in operation there, as if number B is bigger than A (more fit, better adapted to its hypothetical environment) then number A is falsified (de-selected) in the survival contest. (That is how I interpret page 60 of Chaitin 2013, though I may be mistaken.)
Just as further explanation of some of my own epistemological assumptions, I currently subscribe to the Extended Evolutionary Synthesis (eg Pigliucci and Müller 2010).
Mainly as I am interested in Applied Evolutionary Epistemology (eg Gontier 2012).
e.g.: https://storyality.wordpress.com/2013/12/12/storyality-100-the-holonic-structure-of-the-meme-the-unit-of-culture/
and
So this is why it’s important for me to understand this, ie Whether your criticisms are valid. (And they may well be, of course.)
But of course given evolutionary epistemology in general (Campbell etc) I am blissfully unaware of my own unrecognized ignorance…
As an aside, I have my own criticisms of the book, namely the political angle that begins in CH 6, ie the `God’ stuff, the `intelligent design’ interpretation, and secondly while Chaitin talks a lot about biological creativity and creativity in general he never defines the term creativity as he is understanding it; it would be way better in my view if the book cited the standard definition of creativity: eg https://storyality.wordpress.com/2012/12/06/what-is-creativity-and-how-does-it-work/ and also the references need to include DT Campbell, DK Simonton and the systems model of Csikszentmihalyi, as what Chaitin calls randomness in creativity is BVSR (DT Campbell, DK Simonton have published extenisvely on this in the scientific study of creativity in the domains of psychology and sociology and I think it’s an oversight to ignore it all.)
But Chaitin notes Feyerabend’s Against Method is political and he even mentions Israel so he’s happy being political, I have nothing against politics; axiology is important but personally it turns me off from about Ch 6 onwards.
BUT – Artem, if Chaitin’s proof is right, I think, it has massive implications.
(Side note: I’m part Jewish myself – but that’s random chance for you. I am also an atheist.)
Look forward to your thoughts or explanations, if I have missed anything – which is always highly possible.
In summary, my key question is:
If he’s (Chatin) staying with numbers being generated, and then fitness-tested, then, that’s a form of heritability, as (obvious as it sounds here) numbers are still numbers, in the phase-space of possible mutations into: other formal symbol systems.
(eg his mutated critters don’t algorithmically mutate into, words, images, colours, shapes, alphanumeric characters, sentences, novels, jokes, etc)
– Is this not true…?
Note: Though – the irony is, as numbers get bigger, they become more complex, and strange patterns appear, right? (eg numerical palindromes, and primes, cubes, Fibonacci numbers, etc) Chaitin isn’t examining or testing for any of those. But: he could….
ie This is emergence, right? Which possibly explains why consciousness evolves gradually across biological species (eg we apparently are the most conscious but there’s a continuum including dolphins and chimps down to amoebas – and viruses on the borderline/grey area of the emergence of life.)
So – I may well be wrong (and often am), but, I suspect, Chaitin may be a genius. I think his discovery is highly `novel yet appropriate’. (Though, in my own view, it isn’t, technically: surprising. ie This was obviously going to happen on a long enough timeline if the world didnt blow up and humans go extinct, which brings me back to `the problems of religion’.)
ie In my assessment of his accomplishment, I refer to `the standard definition of creativity’ here: (`novel and appropriate’, Simonton added criteria of `surprising’)
http://creativity.netslova.ru/Definitions_of_creativity.html
Let me know – as I suspect you are a lot smarter and more knowledgeable about evolution than I am, and if I am wrong, my theory is screwed, and I will be very annoyed if that’s the case.
ie This theory of mine:
Best
JT
PS – I consider myself a mere layperson in Evolutionary Theory, although, obsessed by it.
Pingback: A detailed update on readership for the first 200 posts | Theory, Evolution, and Games Group
Pingback: Life as Evolving Software | Undefined Terms