Stackexchange and the end of stagnation →

Irreversible evolution with rigor

October 13, 2011 by Julian Xue 2 Comments

We have now seen that man is variable in body and mind; and that the variations are induced, either directly or indreictly, by the same general causes, and obey the same general laws, as with the lower animals.

— First line read on a randomly chosen page of Darwin’s The Descent of Man, in the Chapter “Development of Man from some Lower Form”. But this post isn’t about natural selection at all, so that quote is suitably random.

The intuition of my previous post can be summarized in a relatively inaccurate but simple figure:

In this figure, the number of systems is plotted against the number of components. As the number of components increase from 1 to 2, the number of possible systems greatly increase, due to large size of the space of all components ( $\mathbf{C}$ ). The number of viable systems also increase, since I have yet to introduce a bias against complexity. In the figure, blue are the viable systems, while dashed lines for the 1-systems represent the space of unviable 1-systems.

If we begin at the yellow dot, an addition operation would move it to the lowest red dot. Through a few mutations — movement through the 2-system space — the process will move to the topmost red dot. At this red dot, losing a component is impossible, since losing a component would make it unviable. To lose a component, it would have to back mutate to the bottommost red dot, an event that, although not impossible, is exceedingly unlikely if $\mathbf{C}$ is sufficiently large. This way, the number of components will keep increasing.

The number of components won’t increase without bound, however, as I said in my last post, once $1-(1-p_e)^n$ is large, there is enough arrows emanating from the top red dot (instead of the one arrow in the previous figure) that one of them is likely to hit the viable blues in the 1-systems. At that point, this particular form of increase in complexity will cease.

I’d like to sharpen this model with a bit more rigor. First, however, I want to show a naive approach that doesn’t quite work, at least according to the way that I sold it.

Consider a space of systems $\mathbf{S}$ made up linearly arranged components drawn from $\mathbf{C}$ . Among $\mathbf{S}$ there are viable systems that are uniformly randomly distributed throughout $\mathbf{S}$ ; any $S\in\mathbf{S}$ has a tiny probability $p_v$ of being viable. There is no correlation among viable systems, $p_v$ is the only probability we consider. There are three operations possible on a system S: addition, mutation, and deletion. Addition adds a randomly chosen component from $\mathbf{C}$ to the last spot in S (we will see that the spot is unimportant). Deletion removes a random component from S. Mutation mutates one component of S to another component in $\mathbf{C}$ with uniformly equal probability (that is, any component can mutate to any other component with $\dfrac{1}{|\mathbf{C}|-1}$ probability). Each operation resets $S$ and the result of any operation has $p_v$ of being viable.

Time proceeds in discrete timesteps, at each timstep, the probability of addition, mutation, and deletion are $p_a, p_m$ and $p_d=1-p_a-p_m$ respectively. Let the system at time $t$ be $S_t$ . At each timestep, some operating is performed on $S_t$ , resulting in a new system, call it $R_t$ . If $R_t$ is viable, then there is a probability $p_n$ that $S_{t+1}=R_t$ , else $S_{t+1}=S_t$ . Since the only role that $p_n$ plays is to slow down the process, for now we will consider $p_n=1$ .

Thus, if $S=C_1C_2...C_n$ :

Removal of $C_i$ results in $C_1C_2...C_{i-1}C_{i+1}...C_n$ ,

Addition of a component $B$ results in $C_1C_2...C_nB$

Mutation of a component $C_i$ to another component $B$ results in $C_1C_2...C_{i-1}BC_{i+1}...C_n$

Let the initial S be $S_0=C_v$ , where $C_v$ is viable.

Let $p_v$ be small, but $\dfrac{1}{p_v}<|\mathbf{C}|$ .

The process begins on $C_v$ , additions and mutations are possible. If no additions happen, then in approximately $\dfrac{1}{p_m\cdot p_v}$ time, $C_v$ mutates to another viable component, $B_v$ . Let’s say this happens at time $t$ . Since $p_n=1$ , $S_{t+1}=B_v$ . However, since this changes nothing complexity-wise, we shall not consider it for now.

A successful addition takes approximates $\dfrac{1}{p_a\cdot p_v}$ time. Let this happen at $t_1$ . Then at $t=t_1+1$ , we have $S_{t_1+1}=C_vC_2$ .

At this point, let us consider three possible events. The system can lose $C_v$ , lose $C_2$ , or mutate $C_v$ . Losing $C_2$ results in a viable $C_v$ , and the system restarts. This happens in approximately $\dfrac{2}{p_d}$ time. This will be the most common event, since the chance of resulting in a viable $C_2$ or going through mutation to become a viable $C_3C_2$ are both very low. In fact, $C_vC_2$ must spend $\dfrac{2}{p_mp_v}$ time as itself before it is likely to discover a viable $C_3C_2$ through mutation, or $\dfrac{2}{ p_dp_v}$ before it discovers a viable $C_2$ . The last event isn’t too interesting, since it’s like resetting, but with a viable $C_2$ instead of $C_v$ , which changes nothing (this lower bound is also where Gould’s insight comes from). Finding $C_3C_2$ is interesting, however, since this is potentially the beginning of irreversibility.

Since we need $\dfrac{2}{p_mp_v}$ time as $C_vC_2$ to discover $C_3C_2$ , but each time we discover $C_vC_2$ , it stays that way on average only $\dfrac{2}{p_d}$ time, we must discover $C_vC_2$ $\dfrac{p_d}{p_mp_v}$ times before we have a good chance of discovering a viable $C_3C_2$ . Since it takes $\dfrac{1}{p_a\cdot p_v}$ for each discovery of a viable $C_vC_2$ , in total it will take approximately

$\dfrac{1}{p_a p_v}\cdot\dfrac{p_d}{p_mp_v}=\dfrac{p_d}{p_ap_mp_v^2}$

timsteps before we successfully discover $C_3C_2$ . Phew. For small $p_v$ , we see that it takes an awfully long time before any irreversibility kicks in.

Once we discover a viable $C_3C_2$ , there is $1-(1-p_v)^2$ probability that at least one of $C_3$ and $C_2$ are viable by themselves, in which case a loss can immediately kick in to restart the system again at a single component. The number of timesteps before we discover a viable $C_3C_2$ in which neither are viable by themselves is:

$\dfrac{p_d}{p_ap_mp_v^2(1-(1-p_v)^2)}$ .

Unfortunatly this isn’t quite irreversibility. Now I will show that the time it takes for $C_3C_2$ to reduce down to a viable single component is on the same order as what it takes to find viable $C_3C_4C_5$ or $C_4C_2C_5$ , in which all single deletions (for $C_3C_4C_5$ , the single deletions are: $C_4C_5$ , $C_3C_5$ , and $C_3C_4$ ) are all unviable.

We know that $C_3$ and $C_2$ are unviable on their own. Thus, to lose a component viably, $C_3C_2$ must mutate to $C_3C_v$ (or $C_vC_2$ ), such that $C_3C_v$ (or $C_vC_2$ ) is viable and $C_v$ is also independently viable. To reach a mutant of $C_3C_2$ that is viable takes takes $\dfrac{1}{p_mp_v}$ time. The chance the mutated component will itself be independently viable is $p_v$ . Thus, the approximate time to find one of the viable systems $C_3C_v$ or $C_vC_2$ is $\dfrac{1}{p_mp_v^2}$ . To reach $C_v$ from there takes $\dfrac{2}{p_d}$ time, for a total of

$\dfrac{2}{p_mp_v^2p_d}$

time. It’s quite easy to see that to go from $C_3C_2$ to a three component system (either $C_3C_4C_5$ or $C_4C_2C_5$ ) such that a loss of a component renders the 3-system unviable, is also on the order of $\dfrac{1}{p_v^2}$ time. It takes $\dfrac{1}{p_ap_v}$ to discover the viable 3-system $C_3C_2C_5$ , it then takes $\dfrac{2}{3\cdot p_mp_v}$ time to reach one of $C_3C_4C_5$ or $C_4C_2C_5$ (two thirds of all mutations will hit either $C_3$ or $C_3$ , of these mutation, $p_v$ are viable). Each time a viable 3-system is discovered, the system tends to stay there $\dfrac{3}{p_d}$ time. We must therefore discover viable 3-systems $\dfrac{2p_d}{3\cdot 9p_mp_v}$ times before we have a good chance of discovering a viable 3-system that is locked-in and cannot quickly lose a component, yet remain viable. In total, we need

$\dfrac{2p_d}{9p_mp_ap_v^2}$

time. Since $p_m, p_a, p_d$ are all relatively large numbers (at least compared to $p_v$ ), there is no “force” for the evolution of increased complexity, except the random walk force.

In the next post, I will back up statements with simulations and see how this type of processes allows us to define different types of structure, some of which increases in complexity.

Filed under Analytic, Models, Preliminary, Technical Tagged with evolution, irreversibility

2 Responses to Irreversible evolution with rigor

Artem Kaznatcheev says:

October 13, 2011 at 17:06

You really should find a way to describe this clearly and rigorously with pictures (don’t try to draw graphs of the type you sketch on whiteboards, but instead try a graph theory kind of graph with directed edges labeled by probabilities). I think this will make it easier for you to explain (and maybe even understand) your thoughts more clearly. You’ve presented this to me in person before, and yet I still couldn’t really follow the description in this post. If you are going to throw in random math-jargon, try to be complete with inequalities and such whenever you say something is smaller. Also avoid words like “much larger” or “very very small” unless you are making an approximation in that step (for instance, if you are making a first order approximation of something, you might say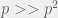 $p >> p^2$ or some such to carry through your argument. Otherwise the words are just distracting.

The most important comment I can make is to figure out where to be general and where not to be general. Could the gist of this had been described with binary strings WLOG? Or where could you have made obvious WLOG assumptions? I think I can see a few places. The best way to do this, I think, is to apply your ideas to concrete models instead of trying to talk about them abstractly.

Reply
Pingback: An update | Theory, Evolution, and Games Group