Algorithmic Darwinism
March 25, 2014 12 Comments
The workshop on computational theories of evolution started off on Monday, March 17th with Leslie Valiant — one of the organizers — introducing his model of evolvability (Valiant, 2009). This original name was meant to capture what type of complexity can be achieved through evolution. Unfortunately — especially at this workshop — evolvability already had a different, more popular meaning in biology: mechanisms that make an organism or species ‘better’ at evolving, in the sense of higher mutations rates, de novo genes, recombination through sex, etc. As such, we need a better name and I am happy to take on the renaming task.
It seems that one of Valiant’s goals in defining his model was to draw a sharp demarcation between the Lamarkian nature of updates in typical machine learning algorithms, and the more limited inter-generational information transfer that he saw as the defining feature of Darwin’s theory. At this he succeeded spectacularly. In fact, I am inclined to say that his conception of evolution is in some ways more restrictive than that of most biologists. For example, the model does not allow one to easily incorporate epigenetics, development, or the effects of individual learning on fitness and thus evolutionary dynamics. It is an extremely strong Darwinism, and the name should reflect this.
In allusion to machine learning, Machine Darwinism is a tempting candidate. However, for many, machine learning is meant to refer to learning by non-biological machines like your laptop or Google’s servers. But Valiant did not set out to just capture in silico evolution, or genetic algorithms. Computational learning theory carries less of this baggage and the extra benefit of Valiant’s central position in the subfield. Unfortunately, the “computational” prefix does not have the connection to theory and mathematics that it could once evoke, instead it suggests the use of computing machines to achieve some goal like simulation or artificial life rather than finding conceptual and formal insights from the theory of computing machines. Thus, we have to rule out Computational Darwinism.
With no surprise given the title, what is left is my preferred modifier — algorithmic. I have already introduced in in the more general context of philosophy and general biology. It carries with it the connections to mathematics and theory, and the focus on dynamics and specific problems. I think it is a great fit, so after this unreasonably long preamble, I will refer to Valiant’s model as Algorithmic Darwinism. I hope he doesn’t mind.
Earlier on TheEGG blog, we already reviewed the basics of algorithmic Darwinism, so I won’t rehash all the details. I will just remind you that it is a way to formally model evolution as a special type of machine learning, a subset of learning through statistical queries. In the second talk of the day, Vitaly Feldman, went into more detail on the relationship between algorithmic Darwinism and machine learning classes (Feldman, 2008). Here, some unfortunately fragility of the model was revealed, a lock of robustness to changes between relatively reasonable loss functions.
On Thursday, Paul Valiant presented the fitness functions for algorithmic Darwinism most clearly as depending on three parameters: the space of target functions, say (other domains and ranges can be considered, for instance the reals (P. Valiant, 2012)), the distribution over inputs D, and the loss function L. Supposing we are trying to evolve the function
and the current organism has a hypothesis
then the fitness is given by an empirical approximation of
given by m samples
from D. Usually, we concentrate on the class of functions F, but it is clear that all three components (along with the mutation operator and class of representations H that define locality) matter for the fitness landscape.
Feldman (2008) showed that if we use the squares loss function then algorithmic Darwinism captures all of statistical query learning (Kearns, 1998). However, if we stick to the correlation loss function that Valiant first considered then the class is equivalent to correlational statistical queries (CSQ) which is known to be a strict subset of SQ (Bshouty & Feldman, 2002). I am not sure how to interpret this discrepancy biology. Regardless of the biological meaning, the connection to known complexity classes has practical significance. Feldman’s results give us a very useful tool. Now we know that any polynomial time CSQ algorithm, no matter how exotic seeming at first, can be transformed into an evolutionary dynamic with the appropriate choice of mutation operator.
 The mutation operator is intimately linked to the organism’s internal representations (or, in machine learning terms: hypotheses class) on which it acts. Although algorithmic Darwinism does not place any specific restrictions on how to interpret the organism’s hypotheses class, the usual story is that they correspond to gene expression levels. Elaine Angelino tasked herself with making the model more appealing to biologists by connecting to a function class that real-world gene expression levels represent. She showed that we can think of gene expression levels as ratios of polynomials and that the transcription networks these polynomials encode have small depth and degree (or, in circuit terms: fan-in). The representations used in Valiant’s and Feldman’s result were more complicated that this.
The mutation operator is intimately linked to the organism’s internal representations (or, in machine learning terms: hypotheses class) on which it acts. Although algorithmic Darwinism does not place any specific restrictions on how to interpret the organism’s hypotheses class, the usual story is that they correspond to gene expression levels. Elaine Angelino tasked herself with making the model more appealing to biologists by connecting to a function class that real-world gene expression levels represent. She showed that we can think of gene expression levels as ratios of polynomials and that the transcription networks these polynomials encode have small depth and degree (or, in circuit terms: fan-in). The representations used in Valiant’s and Feldman’s result were more complicated that this.
Varun Kanade concentrated on the simplest case of these gene regulatory networks, and showed the learnability of sparse linear functions (Angelino & Kanade, 2014). I particularly enjoyed this result in how it jumped around hardness results in a biologically friendly way. In general, approximating sparse linear functions is NP-hard (Natarajan, 1995), but (like most complexity results) the analysis is worst case, which corresponds to very peculiar distributions over instance space. Angelino & Kanade (2014) avoid this by considering only smoothed distributions where they take an arbitrary distribution over and add a little bit of Gaussian noise to each coordinate. This follows the spirit of Spielman & Teng’s (2001,2009) smoothed analysis and is a model that lets us avoid the problems of worst-case results like knife-edge sensitivity. With smoothed distributions, sparse linear functions are learnable with sparse distribution via a very reasonable mutation operator.
Overall, the five talks on algorithmic Darwinism prompted a lot of discussion with a heavy focus on what (if anything) this model says about biology, and how interested biologists should use it. Given the very strong exclusion of non-genetic effects in the model, I was partial to Chrisantha Fernando‘s suggest that this is a good null model, or in cstheory terms: this model should be used for lower-bounds and seperation from more realistic models. However, in a coffee break discussion over cashews, Vitaly Feldman disagreed with my assessment and suggested that for him the connections to other learning classes are really a source of upper-bounds, i.e. a source of evolutionary algorithms for achieving actual tasks. This engineering application never occurred to me, but with reflection it does seem possible that a deeper understanding of algorithmic Darwinism could yield better directed evolution for tasks like drug design or industrial concerns.
This is the second post in a series from the workshop on computational theories of evolution. The previous post was a general introduction.
References
Angelino, E., & Kanade, V. (2014). Attribute-efficient evolvability of linear functions<. In Proceedings of the 5th conference on Innovations in Theoretical Computer Science (pp. 287-300). ACM.
Bshouty, N.H., & Feldman, V. (2002). On using extended statistical queries to avoid membership queries. The Journal of Machine Learning Research, 2: 359-395.
Feldman, V. (2008). Evolvability from learning algorithms. Proceedings of the 40th annual ACM symposium on Theory of Computing, 619-628 DOI: 10.1145/1374376.1374465
Kearns, M. (1998). Efficiently noise tolerant learning from statistical queries. Journal of the ACM, 45(6): 983-1006.
Natarajan, B. K. (1995). Sparse approximate solutions to linear systems. SIAM Journal on Computing, 24(2), 227-234.
Spielman, D., & Teng, S. H. (2001). Smoothed analysis of algorithms: Why the simplex algorithm usually takes polynomial time. In Proceedings of the thirty-third annual ACM symposium on Theory of computing (pp. 296-305). ACM.
Spielman, D. A., & Teng, S. H. (2009). Smoothed analysis: an attempt to explain the behavior of algorithms in practice. Communications of the ACM, 52(10), 76-84.
Valiant, L.G. (2009) Evolvability. Journal of the ACM, 56(1): 3.
Valiant, P. (2012). Distribution free evolvability of polynomial functions over all convex loss functions. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference (pp. 142-148). ACM.

The engineering application never occurred to you? Am I getting this wrong or are we talking about Genetic Algorithms here? Evolutionary design? I remember inviting Chrisanta to give a talk at UCL a few years ago and that’s the sort of thing we were both working on at the time.
No, I wasn’t talking about genetic algorithms, I don’t actually think I completely understood Vitaly’s point. I will try bugging him into elaborating it more. Under applications in the post, I meant actually physically carrying out directed evolution in experimental systems so that the resulting organisms produce some drug you want.
To be perfectly honest, I wouldn’t be all that excited about a theory of genetic algorithms. When I am trying to solve optimization problems, I prefer solvers that were designed with guarantees and optimality analysis in mind. I am not a huge fan of genetic algorithms (or even neural net approaches) for solving engineering problems, although we’ve probably had this discussion before and probably differ in our opinions given your much greater understanding of GAs.
> the model does not allow one to easily incorporate epigenetics, development, or the effects of individual learning on fitness and thus evolutionary dynamics
As Darwinism encompasses these things (except perhaps epigenetics), why would this not be seen as an excellent argument against the use of the term ‘Darwinism’ in the name?
Actually, hardline Darwinism when it was developing was at the same time as a lot of the behaviorist thought was dominant, and it actually specifically took a strong stance against individual learning. This mostly a push-back against Lamarckian thought. My naming is also completely meant as a contrast to Lamarkism. If I wanted to include all of evolution proper, I would have picked a name like “algorithmic evolution”.
You go into a little bit more detail in your reddit comment
Where do I point this out? I specifically say that Darwinism does not include learning, and I say nothing about sexual reproduction. Obviously, I think both (as well as countless other things) are important for evolution, but like I said, if I wanted to evoke all of evolution then I would have used that word. Sexual reproduction (and recombination, etc) is actually within algorithmic Darwinism (i.e. a part of Valiant’s framework), you just include a mutation operator that includes recombination. Easiest way to do this, is if you want to carry some sort of population around then instead of working over the representation space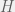 , you can just work over
, you can just work over 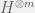 where m is the size of the population you want.
where m is the size of the population you want.
As for sexual selection, that is excluded from this model, as are all frequency-dependent fitness effects. There are probably some ways to hack it in using the above framework, but that is not what the model was built for. This is another good argument for why it should be considered a null case. Of course, there is nothing wrong with trying to understand something simpler like static fitness landscapes before moving on to something more complicated. It is always easy to add features to the point that the model becomes so bloated that you have no hope of understanding any part of it.
I like that, but ‘selection’ doesn’t call biology to mind in the same way. The primary algorithmic knobs on the model are also not related to selection, but to the mutation operator, so it seems like that should feature more prominently in the name. I did toy around with “algorithmic adaptationism” for a while, but didn’t settle down on it. Maybe it is a better name, especially given the prominence of the ‘ideal function’ and the teleological connotations it carries.
great stuff & neat to see valiant is still leading the charge. however have seen you downplay significance of eg genetic algorithms as not connected to real evolution. but it seems these models are at least as abstract and not really closely connected to it.
also, wondering if you know a good review of Valiants popsci book on the subj… do you have one in your blog?
When I saw the term ‘algorithmic Darwinism’: I thought “using genetic/evolutionary ideas to learn algorithms” … and as I work on such a system, I clicked on the link. The normal title for that field is ‘genetic program learning’, I think.
Trying to learn an algorithm is harder than trying to learn a function that describes the end-result of that algo. On the other hand, the result may be more compact, useful: If a dataset is very fractal or chaotic, trying to learn a function that describes the dataset would lead to a big complicated, chaotic function … whereas the underlying algo might be very simple.
Anyway, in nature, biology is mechanical/algorithmic: a sequence of steps taken over time, rather than a function evaluated to obtain a final answer.
What’s wrong with just plain ‘mathematical Darwinism’ or ‘theoretical Darwinism’?
Awesome that this is the thought it brought to mind, because that is exactly the right thought to have. Like all of machine learning, the learning procedure (i.e. evolution in this case) has to learn a function from the domain (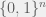 in my post, but could be any other domain) to
in my post, but could be any other domain) to  , with the goal of being with high probability (probably) correct on most inputs (approximately correct). Hence, it is related to genetic programming.
, with the goal of being with high probability (probably) correct on most inputs (approximately correct). Hence, it is related to genetic programming.
Of course, in the cstheory community, genetic programming is famous for not having very deep theory and relying mostly on an experimental and heuristic approach rather than lemma-theorem-proof. It inherits this aversion to theory from genetic algorithm more generally, although obviously there are some provable statements.
As such, it is definitely the case that most classes of functions are too complicated to learn (in fact, for most of the work genetic programming folks work on, you don’t even need complexity or information theory to prove this, it follows from computability). The focus of computational learning theory, and of algorithmic Darwinism is to restrict the function classes enough so that we can prove things about learnability.
That’s a great question! This is a matter of tribes. Most of mathematical and theoretical biology draws its tools from statistics and physics; mathematically and philosophically these tools are very different from the way cstheorists approach questions. As such, using ‘mathematical’ or ‘theoretical’ as a prefix would draw to mind those sort of tools, while we specifically want to draw attention to a difference in methodology. Hence, we need to pick some cstheory related term.
Pingback: Algorithmic Darwinism
Nice post, and sorry for my late comments.
1. Regarding non-robustness to losses. Indeed learning (or evolvability) with correlation loss leads to CSQ which is strictly weaker than learning with quadratic loss that is equivalent to SQ. However there are just two classes SQ and CSQ that can arise as a result of choosing the loss function. The reason for this difference is very simple it’s boolean (or perfectly linear) feedback vs feedback with non-linearities that gives you more information. In reality if the representation is boolean then you get CSQ and if it’s real-valued then the feedback is unlikely to be perfectly linear and you’ll get SQ.
2. In our conversation I was not suggesting to use upper bounds in engineering applications (not that I think that it is impossible, there are plausible scenarios where this type of learning would be useful). In my view upper bounds can inform evolutionary biologists as to which biological mechanisms or phenotypes (expressed as functions of many variables) can easily and routinely evolve and which ones are more likely to be the result of very rare events. For example if we can prove that sparse linear functions are evolvable using some simple mutation mechanism then every phenotype computable by a sparse linear function should not be surprising. Knowing which phenotypes are easy to evolve and how could also guide the research into understanding of biological evolution mechanisms (by analogy I think knowing how machine learning algorithms work is useful in understanding how the human brain could be learning).
Pingback: Cataloging a year of blogging: cancer and biology | Theory, Evolution, and Games Group
Pingback: Mutation-bias driving the evolution of mutation rates | Theory, Evolution, and Games Group
Pingback: Fitness distributions versus fitness as a summary statistic: algorithmic Darwinism and supply-driven evolution | Theory, Evolution, and Games Group