Bounded rationality: systematic mistakes and conflicting agents of mind →

How teachers help us learn deterministic finite automata

September 24, 2013 by Artem Kaznatcheev 4 Comments

Many graduate students, and even professors, have a strong aversion to teaching. This tends to produce awful, one-sided classes that students attend just to transcribe the instructor’s lecture notes. The trend is so bad that in some cases instructors take pride in their bad teaching, and at some institutions — or so I hear around the academic water-cooler — you might even get in trouble for being too good a teacher. Why are you spending so much effort preparing your courses, instead of working on research? And it does take a lot of effort to be an effective teacher, it takes skill to turn a lecture theatre into an interactive environment where information flows both ways. A good teacher has to be able to asses how the students are progressing, and be able to clarify misconceptions held by the students even when the students can’t identify those conceptions as misplaced. Last week I had an opportunity to excercise my teaching by lecturing Prakash Panangaen’s COMP330 course.

Although it might be hard to guess from this blog — with all that discussion of biology, cancer, cognitive science, economics, evolution, philosophy, and social science — that the closest label to what I study officially is probably machine learning and automata theory (I am tempted to throw ‘theoretical’ in front of that, to save myself from writing actual code). As such, on Tuesday I explained a standard automata theory topic — minimizing DFAs, but on Thursday moved onto learning DFAs — a topic seldom covered in an undergraduate automata theory courses (or even in an introductory machine learning course). It was my round-about way of justifying my existence to the students: “I can provide you with counter-examples queries!”

Imagine that we are trying to learn about the world around us, and can run experiments described by strings over $\Sigma$ that yield yes-no answers. Under some philosophical assumptions or — unfortunately for the students — by fiat, we can suppose that this world is described by a regular language $L \subseteq \Sigma^*$ and an experiment $x \in \Sigma^*$ just tells us if $x \in L$ or not. As students of the world, we want to produce a DFA $M$ such that $L(M) = L$ and we want to do this quickly — in time polynomial in the size $n$ of minimal DFA representing $L$ . If we are allowed only membership queries — questions of the form “is $x \in L$ ” — then Angluin (1978) and Gold (1978) showed that this task in NP-hard. Even if we’re allowed to do improper learning and don’t have to output a DFA but can output any machine that will answers questions correctly, the task is at least as hard as cracking the RSA cryptosystem that protects our credit card information online (Kearns & Valiant, 1994; see Lev Reyzin’s blogpost for a more details on the proper-vs-improper learning distinction for automata). In other words, we believe that this is impossible.

Not so if we add a teacher. Angluin (1987) defines a minimal adequate teacher (MAT) as an oracle that can answer counterexample queries. The student can give a candidate DFA $M$ and if $L(M) \neq L$ then the teacher provides a counterexample $z$ such that $z \in L(M)$ but $z \not\in L$ (or vice versa); otherwise the teacher returns “correct” and the student aces her class. Angluin (1987) showed that in the MAT-model model, there exists an algorithm that runs in time polynomial in $n$ and the maximum size $m$ of a counterexample that learns any regular language $L$ . In other words, students be thankful: having a teacher saves you from a combinatorial explosion!

From observation tables to machines

We call a set $S$ prefix closed if for every $w' \in \Sigma^*$ if $ww' \in S$ then $w \in S$ , or — using notation from assignment 1 — if $S = \mathrm{init}(S)$ . We call a finite prefix closed set $S$ , finite set $E$ , and a function $T: (S \cup S.\Sigma).E \rightarrow \{0,1\}$ an observation table. For every $s \in S \cup S.\Sigma$ we define $\mathrm{row}(s): E \rightarrow \{0,1\}$ as $\mathrm{row}(s)(e) = T(se)$ .

An observation table is closed if:

$\forall t \in S.\Sigma \; \exists s \in S \; \mathrm{s.t.} \; \mathrm{row}(t) = \mathrm{row}(s)$

and the observation table is consistent if:

$\forall s_1, s_2 \in S \; \forall a \in \Sigma \quad \mathrm{row}(s_1) = \mathrm{row}(s_2) \Rightarrow \mathrm{row}(s_1a) = \mathrm{row}(s_2a)$

If an observation table is both closed and consistent then we can define a DFA $M(S,E,T)$ based on it, with $Q = \{\mathrm{row}(s) | s \in S\}$ , $q_0 = \mathrm{row}(\epsilon)$ , $Q = \{\mathrm{row}(s) | s \in S \; \mathrm{and} \; T(s) = 1 \}$ , $\delta(\mathrm{row}(s),a) = \mathrm{row}(sa)$ . It might not be obvious that this DFA is well defined, and so it is useful to know two lemmas:

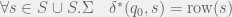
Lemma 1: $\forall s \in S \cup S.\Sigma \quad \delta^*(q_0,s) = \mathrm{row}(s)$

Proof: By induction on length of $s$ .

Lemma 2: $\forall s \in S \cup S.\Sigma \forall e \in E \quad \delta^*(q_0, se) \in F \iff T(se) = 1$

Proof: By induction on length of $e$ with Lemma 1 providing the base case.

Since the machine yields the right result on every entry of $T$ , we say that it is consistent with $T$ . The most important result for the learning algorithm is that this is the smallest DFA consistent with $T$ :

Lemma 3: Suppose that $M(S,E,T)$ has $n$ states. If $M' = (Q',q_0',F',\delta')$ is consistent with $T$ and has $n$ or fewer states then $M'$ is isomorphic to $M(S,E,T)$ .

We will proceed by building an isomorphism $\phi: Q \rightarrow Q'$ between $M'$ and $M$ , defined as $\phi(\mathrm{row(s)}) = \delta'^*(q_0',s)$ . We will show this isomorphism is one-to-one and onto, thus the two machines have the same number of states, and that it preserves initial states, final states, and transitions.

Claim 3.1: $\phi$ is a bijection.

Proof: For all $q' \in Q'$ define $\mathrm{row}(q'): E \rightarrow \{0,1\}$ as $\mathrm{row}(q')(e) = 1 \iff \delta'(q',e) \in F'$ . Since $M'$ is consistent with $T$ , we have for all $s \in S \cup S.\Sigma$ and $e \in E$ :

$\begin{aligned} \delta'^*(q_0,se) \in F' & \iff T(se) = 1 \\ \delta'^*(\delta'^*(q_0,s),e) \in F\ & \iff T(se) = 1 \\ \mathrm{row}(\delta'^*(q_0,s)) & = \mathrm{row}(s) \end{aligned}$

Thus, as $s$ ranges over all of $S$ , $\mathrm{row}(s)$ and thus $\mathrm{row}(q')$ with $q' = \delta'^*(q_0,s)$ takes on $n$ distinct values. If $\mathrm{row}(q') \neq \mathrm{row}(q'')$ then there exists some $e \in E$ such that $\delta'^*(q',e) \neq \delta'^*(q'',e)$ by consistency of $M'$ , thus $M'$ must have $n$ states, and $\phi$ maps every $\mathrm{row}(s)$ to a distinct $q'$ , so the function is a bijection, with $\mathrm{row}: Q' \rightarrow Q$ as its inverse.

Lemma 3.2: $\phi(q_0) = q'_0$ — the function preserves initial states.

Proof: $\phi(q_0) = \phi(\mathrm{row}(\epsilon)) = \delta'^*(q_0',\epsilon) = q_0'$

Lemma 3.3: $\phi(F) = F'$ — the function preserves final states.

Proof: $(\Rightarrow)$ If $\mathrm{row}(s) \in F$ then by definition $T(se) = 1$ but $\mathrm{row}(\phi(\mathrm{row}(s))) = \mathrm{row}(s)$ and $\mathrm{row}(s)(\epsilon) = 1$ so $\phi(\mathrm{row}(s)) \in F'$ by construction.

$(\Leftarrow)$ If $\phi(\mathrm{row}(s)) \in F'$ then since $\mathrm{row}(\phi(\mathrm{row}(s)))) = \mathrm{row}(s)$ and $\mathrm{row}(\phi(\mathrm{row}(s)))(\epsilon) = 1$ , we have $\mathrm{row}(s) \in F$ .

Lemma 3.4 $\phi(\delta(\mathrm{row}(s),a) = \delta'(\phi(\mathrm{row}(s)),a)$ — the function preserves transitions.

Proof: Note that $\forall s \in S, a \in \Sigma$ , since $(S,E,T)$ is closed, there must exist some $s' \in S$ such that $\mathrm{row}(sa) = \mathrm{row}('s)$ . Use that to see:

$\phi(\delta(\mathrm{row}(s),a)) = \phi(\mathrm{row}(sa)) = \phi(\mathrm{row}(s') = \delta'^*(q_0',s')$ , and

$\delta'(\phi(\mathrm{row}(s)),a) = \delta'(\delta'^*(q_0,s),a) = \delta'^*(q_0',sa)$

But $\mathrm{row}(\delta'^*(q_0',s')) = \mathrm{row}(\delta'^*(q_0',sa))$ , so the two states are the same.

Angluin-Schapire learning algorithm

Angluin (1987) provided a nice algorithm for learning DFAs using observation tables, but it is no longer the best known algorithm. In his thesis, Schapire (1991) presented an improved algorithm that I will sketch here. This algorithm will never have a non-consistent table, and will add only one element to $E$ per counterexample using a special subroutine find_extend.

Initalize S & E to $\{ \epsilon \}$
Ask membership queries for $\epsilon$ and each $a \in \Sigma$
Construct the initial observation table (S,E,T)
Repeat until teacher says “Correct”:
1. While (S,E,T) is not closed:
  1. Find $s' \in S$ and $a \in \Sigma$ such that $\forall s \in S \quad \mathrm{row}(s) \neq \mathrm{row}(s'a)$ .
  2. Add $s'a$ to $S$ and extend T using membership queries.
2. Let $M = M(S,E,T)$ and ask teach if M is correct.
3. If the teacher replies with a counter-example z, then let $e \leftarrow \mathrm{find\_extend}(z,M)$ , add $e$ to E and extend T using membership queries.
Return M and Halt

The last ingredient is find_extend, which will return a counter-example that can serve as a witness to separate two states we previously thought to be equivalent. In particular, it will return and $e$ such that:

$\exists s, s' \in S \; a \in \Sigma \; \mathrm{with}\; \mathrm{row}(s) = \mathrm{row}(s'a) \; \mathrm{and} \; L(se) \neq L(s'ae)$

find_extend(z,M):

Using lazy evaluation, consider the partitions $z = p_i r_i$ for every $latex 0 \leq |p_i| = i \leq |z| = m.
Using lazy evaluation, let $s_i$ be the state of M if you run it on $p_i$ , i.e. such that $\delta^*(s_0,p_i) = \mathrm{row}(s_i)$
Notice that $L(s_0r_0) = L(z) \neq L_M(z) = L(s_mr_m)$ because z is a counter-example
Since the two extreme values of $i$ have different results, there must be some $k$ such that $L(s_kr_k) \neq L(s_{k+1}r_{k+1}$ . Find such a $k$ using binary search.
Return $r_{k + 1}$ .

I leave it to the reader to implement the binary search and achieve a number of membership queries equal to $O(\log m)$ (where $m$ is the size of the largest counterexample) for each run of find_extend and to check that the returned value satisfies the condition we want. Since this returned $e$ is a witness to the difference of two previously equal states, we know that the observation table will no longer be closed and we will have to add at least one more state to the candidate machine. Since the candidate machine is always the smallest that is consistent with T, and since T always agrees with the finite subset of L that it has sampled, it must be the case that the algorithm stops doing counter-example queries when the number of states reaches the number of states $n$ in the minimal DFA representing the regular language to be learned. Thus, the algorithm requires up to $n$ counterexample queries and $O(n^2 + n\log m)$ membership queries.

References

Angluin, D. (1978). On the complexity of minimum inference of regular sets. Information and Control, 3(39):337–350.

Angluin, D. (1987). Learning regular sets from queries and counterexamples. Information and Computation,, 75, 87-106 DOI: 10.1016/0890-5401(87)90052-6

Gold, E.M. (1978). Complexity of automaton identification from given data. Information and Control, 3(37):302–420.

Kearns, M., & Valiant, L. (1994). Cryptographic limitations on learning Boolean formulae and finite automata. Journal of the ACM, 41(1), 67-95.

Schapire, R. E. (1991). The design and analysis of efficient learning algorithms. (No. MIT/LCS/TR-493) MIT, Cambridge, USA

Filed under Reviews, Technical Tagged with cstheory, finite state automata, Leslie Valiant, machine learning

About Artem Kaznatcheev
From the Department of Computer Science at Oxford University and Department of Translational Hematology & Oncology Research at Cleveland Clinic, I marvel at the world through algorithmic lenses. My mind is drawn to evolutionary dynamics, theoretical computer science, mathematical oncology, computational learning theory, and philosophy of science. Previously I was at the Department of Integrated Mathematical Oncology at Moffitt Cancer Center, and the School of Computer Science and Department of Psychology at McGill University. In a past life, I worried about quantum queries at the Institute for Quantum Computing and Department of Combinatorics & Optimization at University of Waterloo and as a visitor to the Centre for Quantum Technologies at National University of Singapore. Meander with me on Google+ and Twitter.